| NCERT Exemplar Solutions | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 9 Areas Of Parallelograms And Triangles
Welcome to this dedicated resource providing comprehensive solutions and detailed explanations for the NCERT Exemplar problems designed for Class 9 students, specifically focusing on the crucial geometry chapter: Areas of Parallelograms and Triangles. This section moves significantly beyond basic formula application, delving into the core conceptual understanding required by the Exemplar questions. These problems are meticulously crafted to challenge students, emphasizing the rigorous application of area theorems within often complex geometric configurations and demanding logical proof construction rather than mere calculation. Mastering these solutions will significantly enhance your grasp of geometric reasoning and proof techniques related to area.
The foundation of this chapter rests upon a set of fundamental theorems concerning area comparisons. These are not just rules to be memorized but principles to be understood and applied strategically. The core concepts you will encounter and need to master include:
- The theorem stating that parallelograms which share the same base (or equal bases) and lie between the same parallel lines are equal in area. This forms a cornerstone for comparing the areas of quadrilateral figures under specific conditions.
- A parallel theorem for triangles: Triangles positioned on the same base (or equal bases) and confined between the same parallel lines possess equal areas. This is vital for many proofs involving triangular sections of larger figures.
- The critical relationship connecting triangles and parallelograms: The area of a triangle is precisely $\frac{1}{2}$ the area of any parallelogram that stands on the same base and is situated between the same parallel lines.
- An essential property related to triangle medians: A median of a triangle divides the triangle into two smaller triangles that have exactly equal areas. This property is frequently exploited in problems involving triangle subdivisions.
Successfully tackling the NCERT Exemplar problems demands more than just knowing these theorems; it requires a keen eye for geometric detail. Students must develop the ability to skillfully identify relevant parallelograms and triangles within intricate diagrams that satisfy the specific conditions (same base, same parallels) laid out in the theorems. The challenge often lies in applying these theorems—sometimes multiple times or in clever combinations—to establish proofs regarding the equality of areas or specific area relationships between different parts of a complex figure. You will frequently encounter problems involving the properties of parallelogram diagonals (dividing the parallelogram into triangles of equal area) or the implications of medians and centroids concerning area division within triangles.
The Exemplar presents these challenges through various question formats. You will find Multiple Choice Questions (MCQs) testing quick application or comparison, Fill-in-the-Blanks reinforcing key facts, True/False statements probing the precise conditions of theorems, and, most significantly, Short and Long Answer questions. These latter types demand rigorous, step-by-step proofs to establish area equalities or ratios, requiring meticulous justification based explicitly on the area theorems learned. The provided solutions are designed to illuminate this process, featuring clear diagrams that highlight the pertinent bases and parallels, logical step-by-step proof structures citing the specific theorems used at each stage, and systematic methodologies for comparing areas even in figures composed of multiple shapes. This resource aims to empower students to confidently navigate the theoretical nuances of area comparison and apply them proficiently in formal geometric proofs.
Sample Question 1 (Before Exercise 9.1)
Write the correct answer:
Sample Question 1: The area of the figure formed by joining the mid-points of the adjacent sides of a rhombus with diagonals 12 cm and 16 cm is
(A) 48 cm2
(B) 64 cm2
(C) 96 cm2
(D) 192 cm2
Answer:
Solution: The correct option is (A) 48 cm2.
Let's break down the solution step-by-step.
Given:
A rhombus ABCD.
Length of the diagonal, $AC = 12$ cm.
Length of the other diagonal, $BD = 16$ cm.
P, Q, R, and S are the mid-points of the sides AB, BC, CD, and DA respectively.
To Find:
The area of the quadrilateral PQRS.
Solution:
We use the Mid-point Theorem, which states that the line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is half of it.
In $\triangle ABC$, P and Q are the mid-points of sides AB and BC respectively.
Therefore, by the Mid-point Theorem:
$PQ \parallel AC$ and $PQ = \frac{1}{2} AC$
... (i)
$PQ = \frac{1}{2} \times 12 = 6$ cm.
Similarly, in $\triangle ADC$, S and R are the mid-points of sides AD and CD respectively.
Therefore, by the Mid-point Theorem:
$SR \parallel AC$ and $SR = \frac{1}{2} AC$
... (ii)
$SR = \frac{1}{2} \times 12 = 6$ cm.
From (i) and (ii), we have $PQ \parallel SR$ and $PQ = SR = 6$ cm.
Since one pair of opposite sides is equal and parallel, PQRS is a parallelogram.
Now, in $\triangle ABD$, P and S are the mid-points of sides AB and AD respectively.
Therefore, by the Mid-point Theorem:
$PS \parallel BD$ and $PS = \frac{1}{2} BD$
... (iii)
$PS = \frac{1}{2} \times 16 = 8$ cm.
We know that the diagonals of a rhombus are perpendicular to each other. So, $AC \perp BD$.
Since $PQ \parallel AC$ and $PS \parallel BD$, the angle between PQ and PS must be the same as the angle between AC and BD.
Therefore, $PQ \perp PS$, which means $\angle QPS = 90^\circ$.
A parallelogram with one angle of $90^\circ$ is a rectangle. Thus, PQRS is a rectangle.
The area of rectangle PQRS is given by:
Area = length $\times$ breadth
Area of PQRS = $PS \times PQ$
Area of PQRS = $8 \text{ cm} \times 6 \text{ cm} = 48 \text{ cm}^2$.
Alternate Solution:
A property of quadrilaterals states that the area of the figure formed by joining the mid-points of the adjacent sides of a quadrilateral is half the area of the original quadrilateral.
Area of PQRS = $\frac{1}{2} \times$ Area of rhombus ABCD.
First, we find the area of the rhombus ABCD.
Area of a rhombus = $\frac{1}{2} \times d_1 \times d_2$, where $d_1$ and $d_2$ are the diagonals.
Area of rhombus ABCD = $\frac{1}{2} \times AC \times BD$
Area of rhombus ABCD = $\frac{1}{2} \times 12 \text{ cm} \times 16 \text{ cm}$
Area of rhombus ABCD = $96 \text{ cm}^2$.
Now, we can find the area of PQRS:
Area of PQRS = $\frac{1}{2} \times 96 \text{ cm}^2$
Area of PQRS = $48 \text{ cm}^2$.
Hence, the area of the figure formed is 48 cm2, which corresponds to option (A).
Exercise 9.1
Write the correct answer in each of the following :
Question 1. The median of a triangle divides it into two
(A) triangles of equal area
(B) congruent triangles
(C) right triangles
(D) isosceles triangles
Answer:
Solution: The correct option is (A) triangles of equal area.
Here is a detailed explanation of why a median of a triangle divides it into two triangles of equal area.
Given:
A $\triangle ABC$ in which AD is the median to the side BC. Since AD is the median, D is the mid-point of BC.
Therefore, $BD = CD$.
To Prove:
Area($\triangle ABD$) = Area($\triangle ADC$)
Construction:
Draw a perpendicular from vertex A to the side BC, meeting BC at point E. Let this altitude be $AE = h$.
Proof:
We know that the area of a triangle is given by the formula:
Area = $\frac{1}{2} \times \text{base} \times \text{height}$
Now, let's calculate the area of $\triangle ABD$.
For $\triangle ABD$, the base is BD and the height is AE (h).
Area($\triangle ABD$) = $\frac{1}{2} \times BD \times AE$
... (i)
Next, let's calculate the area of $\triangle ADC$.
For $\triangle ADC$, the base is CD and the height is also AE (h), since both triangles share the same vertex A and their bases lie on the same straight line BC.
Area($\triangle ADC$) = $\frac{1}{2} \times CD \times AE$
... (ii)
From the given information, we know that AD is the median, which means D is the mid-point of BC.
BD = CD
... (iii)
From equations (i), (ii), and (iii), we can conclude that:
Area($\triangle ABD$) = Area($\triangle ADC$)
Thus, a median of a triangle divides it into two triangles of equal area.
Analysis of Other Options:
(B) Congruent triangles: The two triangles are congruent only if the original triangle is isosceles (with $AB=AC$) or equilateral. For a general scalene triangle, they are not congruent.
(C) Right triangles: This is not generally true. The triangles formed would only be right triangles if the median AD is also an altitude (i.e., $AD \perp BC$), which is a special case for isosceles and equilateral triangles.
(D) Isosceles triangles: The triangles formed by the median are not necessarily isosceles triangles.
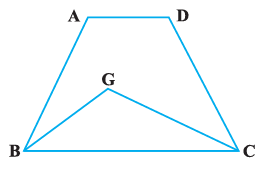
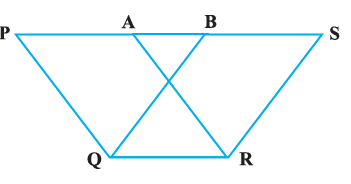
Question 2. In which of the following figures (Fig. 9.3), you find two polygons on the same base and between the same parallels?
(A)

(B)
(C)

(D)
Answer:
To identify the correct figure, we need to find one where two polygons satisfy two specific conditions:
1. Same Base: The two polygons must share a common side, which serves as their base.
2. Between the Same Parallels: The vertices of the polygons that are opposite to this common base must all lie on a single straight line that is parallel to the base.
Let's analyze each of the four figures based on these two conditions.
Analysis of the Figures:
Figure (A):
This figure shows a parallelogram PQRS and another polygon inside it. While they might share a base (e.g., PS), the vertices of the inner polygon opposite to the base do not lie on the line QR, which is parallel to PS. Therefore, this figure does not meet the second condition.
Figure (B):
This figure shows a trapezium ABCD and a triangle GBC. They share a common base BC. For them to be between the same parallels, the vertices opposite the base (A and D for the trapezium, and G for the triangle) must all lie on a line parallel to BC. While the line AD is parallel to BC, the vertex G of the triangle does not lie on the line AD. Thus, the condition is not met.
Figure (C):
This figure shows a parallelogram PQRS and a triangle with base QR. They share the common base QR. However, the vertex of the triangle opposite to the base QR does not lie on the line PS, which is parallel to QR. Therefore, this figure does not satisfy the second condition.
Figure (D):
This figure shows a trapezium where PS is parallel to QR. Within this figure, we can identify two parallelograms: $PARQ$ and $BSRQ$.
- Same Base: Both parallelograms, $PARQ$ and $BSRQ$, share the common base QR.
- Between the Same Parallels: The vertices opposite to the base QR are P and S, respectively. Both of these vertices lie on the straight line PS. The figure indicates that the line segment PS is parallel to the base QR.
Since both conditions are met for parallelograms PARQ and BSRQ, this is the correct figure.
Therefore, the figure that shows two polygons on the same base and between the same parallels is (D).
Question 3. The figure obtained by joining the mid-points of the adjacent sides of a rectangle of sides 8 cm and 6 cm is :
(A) a rectangle of area 24 cm2
(B) a square of area 25 cm2
(C) a trapezium of area 24 cm2
(D) a rhombus of area 24 cm2
Answer:
Solution: The correct option is (D) a rhombus of area 24 cm2.
Here is a detailed explanation of the solution.
Given:
A rectangle ABCD.
Length of the rectangle, $CD = AB = 8$ cm.
Breadth of the rectangle, $BC = DA = 6$ cm.
E, F, G, and H are the mid-points of the sides AB, BC, CD, and DA respectively.
To Find:
The type of figure obtained by joining the points E, F, G, H and its area.
Construction:
Join the diagonals of the rectangle, AC and BD.
Solution:
First, we will determine the type of quadrilateral EFGH. We will use the Mid-point Theorem.
In $\triangle ABC$, E and F are the mid-points of sides AB and BC.
By the Mid-point Theorem:
$EF \parallel AC$ and $EF = \frac{1}{2} AC$
... (i)
Similarly, in $\triangle ADC$, H and G are the mid-points of sides AD and CD.
By the Mid-point Theorem:
$HG \parallel AC$ and $HG = \frac{1}{2} AC$
... (ii)
From (i) and (ii), we can conclude that $EF \parallel HG$ and $EF = HG$. Since one pair of opposite sides is equal and parallel, EFGH is a parallelogram.
Now, let's find the length of the diagonal AC using the Pythagoras theorem in the right-angled $\triangle ABC$.
$AC^2 = AB^2 + BC^2$
$AC^2 = 8^2 + 6^2 = 64 + 36 = 100$
$AC = \sqrt{100} = 10$ cm.
The diagonals of a rectangle are equal in length, so $BD = AC = 10$ cm.
Now, let's look at the other pair of sides of EFGH. In $\triangle ABD$, E and H are the mid-points of AB and AD.
By the Mid-point Theorem:
$EH = \frac{1}{2} BD$
... (iii)
We have $EF = \frac{1}{2} AC$ and $EH = \frac{1}{2} BD$. Since $AC = BD$, it follows that $EF = EH$.
A parallelogram with adjacent sides equal is a rhombus. Therefore, EFGH is a rhombus.
Now, we find the area of the rhombus EFGH.
The diagonals of the rhombus EFGH are EG and FH. From the figure, we can see that the length of diagonal EG is equal to the breadth of the rectangle (BC), and the length of diagonal FH is equal to the length of the rectangle (AB).
$EG = BC = 6$ cm
$FH = AB = 8$ cm
Area of a rhombus = $\frac{1}{2} \times (\text{product of diagonals})$
Area of rhombus EFGH = $\frac{1}{2} \times EG \times FH$
Area of rhombus EFGH = $\frac{1}{2} \times 6 \times 8 = 24 \text{ cm}^2$.
So, the figure is a rhombus with an area of 24 cm2.
Alternate Solution:
A known property states that the area of the figure formed by joining the mid-points of the sides of a quadrilateral is half the area of the original quadrilateral.
First, calculate the area of the rectangle ABCD.
Area of rectangle ABCD = length $\times$ breadth
Area of rectangle ABCD = $8 \text{ cm} \times 6 \text{ cm} = 48 \text{ cm}^2$.
Now, the area of the quadrilateral EFGH is:
Area of EFGH = $\frac{1}{2} \times$ Area of rectangle ABCD
Area of EFGH = $\frac{1}{2} \times 48 \text{ cm}^2 = 24 \text{ cm}^2$.
Also, the quadrilateral formed by joining the mid-points of the sides of a rectangle is always a rhombus.
Therefore, the resulting figure is a rhombus of area 24 cm2.
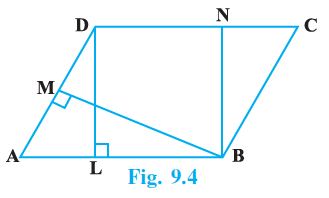
Question 4. In Fig. 9.4, the area of parallelogram ABCD is :
(A) AB × BM
(B) BC × BN
(C) DC × DL
(D) AD × DL
Answer:
Solution: The correct option is (C) DC × DL.
Given:
A parallelogram ABCD.
From the figure, DL is the altitude to the side AB, which means $DL \perp AB$.
Also, BM is the altitude to the side AD, which means $BM \perp AD$.
To Find:
The correct expression for the area of parallelogram ABCD from the given options.
Solution:
The formula for the area of a parallelogram is given by the product of its base and the corresponding altitude (height).
Area of Parallelogram = Base $\times$ Corresponding Height
We can calculate the area of parallelogram ABCD in two ways based on the given altitudes:
1. Taking AB as the base:
The corresponding altitude to the base AB is DL.
Therefore, Area(ABCD) = $AB \times DL$.
2. Taking AD as the base:
The corresponding altitude to the base AD is BM.
Therefore, Area(ABCD) = $AD \times BM$.
We also know that in a parallelogram, opposite sides are equal in length.
So, $AB = DC$ and $AD = BC$.
Using these properties, we can write the area formulas as:
Area(ABCD) = $DC \times DL$ (since $AB = DC$)
Area(ABCD) = $BC \times BM$ (since $AD = BC$)
Analysis of Options:
Let's check each option against our derived formulas.
(A) AB × BM: This is incorrect. It multiplies the base AB with the altitude BM, which corresponds to the base AD, not AB.
(B) BC × BN: This is incorrect. There is no altitude named BN shown in the figure. Even if we consider the formula $BC \times BM$, this option is different.
(C) DC × DL: This is correct. As shown above, since $AB = DC$, the area formula $AB \times DL$ can be written as $DC \times DL$.
(D) AD × DL: This is incorrect. It multiplies the base AD with the altitude DL, which corresponds to the base AB, not AD.
Therefore, the only correct expression for the area of the parallelogram is DC × DL.
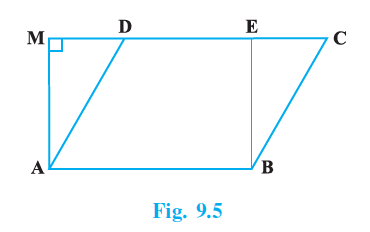
Question 5. In Fig. 9.5, if parallelogram ABCD and rectangle ABEF are of equal area, then :
(A) Perimeter of ABCD = Perimeter of ABEM
(B) Perimeter of ABCD < Perimeter of ABEM
(C) Perimeter of ABCD > Perimeter of ABEM
(D) Perimeter of ABCD = $\frac{1}{2}$ (Perimeter of ABEM)
Answer:
Solution: The correct option is (C) Perimeter of ABCD > Perimeter of ABEM.
Given:
A parallelogram ABCD and a rectangle ABEM are on the same base AB.
The area of parallelogram ABCD is equal to the area of rectangle ABEM.
From the figure, this implies they lie between the same parallel lines AB and MC. AM is the height for both figures.
To Find:
The relationship between the perimeter of parallelogram ABCD and the perimeter of rectangle ABEM.
Solution:
The perimeter of the parallelogram ABCD is given by:
Perimeter(ABCD) = $AB + BC + CD + DA$
The perimeter of the rectangle ABEM is given by:
Perimeter(ABEM) = $AB + BE + EM + MA$
Since ABCD is a parallelogram, its opposite sides are equal.
$CD = AB$
... (i)
Since ABEM is a rectangle, its opposite sides are equal.
$EM = AB$
... (ii)
From equations (i) and (ii), we have $CD = EM$.
Now, let's compare the other sides. Consider the right-angled triangle $\triangle AMD$ (right-angled at M as AM is part of the rectangle).
In a right-angled triangle, the hypotenuse is the longest side. Here, AD is the hypotenuse.
$AD > AM$
... (iii)
Similarly, consider the right-angled triangle $\triangle BEC$ (right-angled at E as BE is part of the rectangle).
In this triangle, BC is the hypotenuse.
$BC > BE$
... (iv)
Now, adding the inequalities (iii) and (iv):
$AD + BC > AM + BE$
Let's add $AB + AB$ to both sides of the inequality:
$AB + AB + AD + BC > AB + AB + AM + BE$
Using the properties from equations (i) and (ii), we can replace one AB on the left with CD and one AB on the right with EM.
$(AB + CD) + (AD + BC) > (AB + EM) + (AM + BE)$
This is the comparison of the perimeters:
Perimeter of ABCD > Perimeter of ABEM
Therefore, the perimeter of the parallelogram is greater than the perimeter of the rectangle.
Question 6. The mid-point of the sides of a triangle along with any of the vertices as the fourth point make a parallelogram of area equal to
(A) $\frac{1}{2}$ ar (ABC)
(B) $\frac{1}{3}$ ar (ABC)
(C) $\frac{1}{4}$ ar (ABC)
(D) ar (ABC)
Answer:
Solution: The correct option is (A) $\frac{1}{2}$ ar (ABC).
Here is a detailed explanation of the solution.
Given:
A triangle $\triangle ABC$.
D, E, and F are the mid-points of the sides BC, CA, and AB respectively.
To Find:
The area of a parallelogram formed by joining the mid-points and any one vertex of the triangle, in relation to the area of $\triangle ABC$.
Solution:
By the Mid-point Theorem, the line segment joining the mid-points of two sides of a triangle is parallel to the third side and is half of it.
In $\triangle ABC$:
$FE \parallel BC$ and $FE = \frac{1}{2} BC = BD = DC$
$DE \parallel AB$ and $DE = \frac{1}{2} AB = AF = FB$
$FD \parallel AC$ and $FD = \frac{1}{2} AC = AE = EC$
Since the opposite sides are parallel, AFDE, BDFE, and CDGE are all parallelograms.
A key property derived from this is that when the mid-points of the sides of a triangle are joined, the triangle is divided into four smaller triangles of equal area.
ar($\triangle AFE$) = ar($\triangle BFD$) = ar($\triangle CDE$) = ar($\triangle DEF$)
... (i)
The total area of $\triangle ABC$ is the sum of the areas of these four triangles:
ar($\triangle ABC$) = ar($\triangle AFE$) + ar($\triangle BFD$) + ar($\triangle CDE$) + ar($\triangle DEF$)
ar($\triangle ABC$) = 4 $\times$ ar($\triangle DEF$)
This implies:
ar($\triangle DEF$) = $\frac{1}{4}$ ar($\triangle ABC$)
... (ii)
Now, let's consider the parallelogram formed by the mid-points F, D, E and the vertex A, which is the parallelogram AFDE.
The diagonal FD divides the parallelogram AFDE into two triangles of equal area, $\triangle AFE$ and $\triangle FDE$. (Note: FDE is the same as DEF).
Area of parallelogram AFDE = ar($\triangle AFE$) + ar($\triangle DEF$)
Using the property from equation (i) that ar($\triangle AFE$) = ar($\triangle DEF$), we can write:
Area of parallelogram AFDE = ar($\triangle DEF$) + ar($\triangle DEF$)
Area of parallelogram AFDE = 2 $\times$ ar($\triangle DEF$)
Now, substituting the value of ar($\triangle DEF$) from equation (ii):
Area of parallelogram AFDE = $2 \times \left(\frac{1}{4} \text{ ar}(\triangle ABC)\right)$
Area of parallelogram AFDE = $\frac{2}{4}$ ar($\triangle ABC$)
Area of parallelogram AFDE = $\frac{1}{2}$ ar($\triangle ABC$)
The same logic applies to the other parallelograms BDFE and CDGE. Thus, the area of a parallelogram formed by the mid-points of the sides of a triangle along with any of the vertices is equal to half the area of the original triangle.
Question 7. Two parallelograms are on equal bases and between the same parallels. The ratio of their areas is
(A) 1 : 2
(B) 1 : 1
(C) 2 : 1
(D) 3 : 1
Answer:
Solution: The correct option is (B) 1 : 1.
Theorem Statement:
This question is a direct application of a fundamental theorem in geometry which states: Parallelograms on the same base or on equal bases and between the same parallels are equal in area.
Given:
Let there be two parallelograms, say $P_1$ and $P_2$.
Let the base of $P_1$ be $b_1$ and its area be $A_1$.
Let the base of $P_2$ be $b_2$ and its area be $A_2$.
According to the problem:
1. The parallelograms are on equal bases, so $b_1 = b_2$.
2. They are between the same parallels, which means their corresponding altitudes (heights) are equal. Let the height of $P_1$ be $h_1$ and the height of $P_2$ be $h_2$. So, $h_1 = h_2$.
To Find:
The ratio of their areas, i.e., $A_1 : A_2$.
Solution:
The formula for the area of a parallelogram is:
Area = Base $\times$ Height
For the first parallelogram, $P_1$:
$A_1 = b_1 \times h_1$
... (i)
For the second parallelogram, $P_2$:
$A_2 = b_2 \times h_2$
... (ii)
From the given conditions, we have:
$b_1 = b_2$
(Given: equal bases)
$h_1 = h_2$
(Given: between same parallels)
Let $b_1 = b_2 = b$ and $h_1 = h_2 = h$.
Substituting these into equations (i) and (ii), we get:
$A_1 = b \times h$
$A_2 = b \times h$
From this, it is clear that $A_1 = A_2$.
Now, let's find the ratio of their areas:
Ratio = $\frac{A_1}{A_2} = \frac{b \times h}{b \times h} = \frac{1}{1}$
Therefore, the ratio of their areas is 1 : 1.
Question 8. ABCD is a quadrilateral whose diagonal AC divides it into two parts, equal in area, then ABCD
(A) is a rectangle
(B) is always a rhombus
(C) is a parallelogram
(D) need not be any of (A), (B) or (C)
Answer:
Solution: The correct option is (D) need not be any of (A), (B) or (C).
Given:
A quadrilateral ABCD where the diagonal AC divides it into two triangles of equal area.
ar($\triangle ABC$) = ar($\triangle ADC$)
To Find:
The specific type of quadrilateral that ABCD must be.
Solution:
The area of a triangle is given by the formula: Area = $\frac{1}{2} \times \text{base} \times \text{height}$.
Let's consider the diagonal AC as the common base for both triangles, $\triangle ABC$ and $\triangle ADC$.
Let's draw perpendiculars from vertices B and D to the diagonal AC. Let these be BE and DF, so BE and DF are the heights of $\triangle ABC$ and $\triangle ADC$ respectively.
Area of $\triangle ABC = \frac{1}{2} \times AC \times BE$
Area of $\triangle ADC = \frac{1}{2} \times AC \times DF$
Since we are given that the areas are equal:
$\frac{1}{2} \times AC \times BE = \frac{1}{2} \times AC \times DF$
This implies that $BE = DF$.
So, the given condition means that the perpendicular distance from vertex B to the diagonal AC is equal to the perpendicular distance from vertex D to the diagonal AC.
Analysis of Options:
(A) is a rectangle, (B) is always a rhombus, (C) is a parallelogram:
All parallelograms (which include rectangles, rhombuses, and squares) have the property that a diagonal divides them into two congruent triangles. Since congruent triangles have equal areas, all these figures satisfy the given condition.
However, the question asks what ABCD must be given this condition. We need to check if any quadrilateral that satisfies this condition must be a parallelogram.
Counterexample:
Consider a kite where the diagonal AC is an axis of symmetry. In such a kite, $\triangle ABC$ is congruent to $\triangle ADC$. Therefore, their areas are equal. However, a kite is not a parallelogram (unless it is a rhombus). Since a kite satisfies the condition but is not necessarily a parallelogram, rectangle, or rhombus, options (A), (B), and (C) are incorrect.
Even a more general quadrilateral can be constructed. As long as the vertices B and D are equidistant from the line containing the diagonal AC, the areas of $\triangle ABC$ and $\triangle ADC$ will be equal. This does not force the quadrilateral to be a parallelogram.
Therefore, a quadrilateral whose diagonal divides it into two parts of equal area need not be a rectangle, rhombus, or parallelogram.
Question 9. If a triangle and a parallelogram are on the same base and between same parallels, then the ratio of the area of the triangle to the area of parallelogram is
(A) 1 : 3
(B) 1 : 2
(C) 3 : 1
(D) 1 : 4
Answer:
Explanation:
The area of a triangle is given by the formula:
$\text{Area of triangle} = \frac{1}{2} \times \text{Base} \times \text{Height}$
The area of a parallelogram is given by the formula:
$\text{Area of parallelogram} = \text{Base} \times \text{Height}$
We are given that the triangle and the parallelogram are on the same base. Let the length of this common base be $b$.
We are also given that the triangle and the parallelogram are between the same parallels. When two figures are between the same parallels, their heights (altitudes) corresponding to the bases on one of the parallel lines are equal. Let this common height be $h$.
Using the formulas with the common base $b$ and common height $h$:
Area of the triangle = $\frac{1}{2} \times b \times h$
Area of the parallelogram = $b \times h$
The ratio of the area of the triangle to the area of the parallelogram is:
$\frac{\text{Area of triangle}}{\text{Area of parallelogram}} = \frac{\frac{1}{2} \times b \times h}{b \times h}$
Assuming $b \neq 0$ and $h \neq 0$, we can cancel the common terms $b \times h$ from the numerator and the denominator:
$\frac{\text{Area of triangle}}{\text{Area of parallelogram}} = \frac{\frac{1}{2}}{1}$
$\frac{\text{Area of triangle}}{\text{Area of parallelogram}} = \frac{1}{2}$
Thus, the ratio of the area of the triangle to the area of the parallelogram is 1 : 2.
The correct answer is (B) 1 : 2.
Question 10. ABCD is a trapezium with parallel sides AB = a cm and DC = b cm (Fig. 9.6). E and F are the mid-points of the non-parallel sides. The ratio of ar (ABFE) and ar (EFCD) is

(A) a : b
(B) (3a + b) : (a + 3b)
(C) (a + 3b) : (3a + b)
(D) (2a + b) : (3a + b)
Answer:
Solution: The correct option is (B) (3a + b) : (a + 3b).
Given:
A trapezium ABCD with $AB \parallel DC$.
Length of side $AB = a$ cm.
Length of side $DC = b$ cm.
E and F are the mid-points of the non-parallel sides AD and BC respectively.
To Find:
The ratio of ar(ABFE) and ar(EFCD).
Construction:
Draw a perpendicular from D to the side AB, let's call it DL. This line DL represents the height of the trapezium ABCD. Let the line segment EF intersect DL at point P.
Solution:
First, we need to find the length of the line segment EF. The line segment joining the mid-points of the non-parallel sides of a trapezium is parallel to the parallel sides and its length is half the sum of the lengths of the parallel sides.
$EF = \frac{1}{2} (AB + DC)$
$EF = \frac{a+b}{2}$
... (i)
Since E is the mid-point of AD and $EP \parallel AL$ (as $EF \parallel AB$), P is the mid-point of the height DL. This means the height of the trapezium EFCD (which is DP) is equal to the height of the trapezium ABFE (which is PL).
Let the height of trapezium ABCD be $2h$. Then, the height of trapezium ABFE is $h$ and the height of trapezium EFCD is also $h$.
Now, we calculate the area of the trapezium ABFE. The area of a trapezium is given by the formula:
Area = $\frac{1}{2} \times (\text{sum of parallel sides}) \times (\text{height})$
ar(ABFE) = $\frac{1}{2} \times (AB + EF) \times h$
Substituting the values of AB and EF:
ar(ABFE) = $\frac{1}{2} \times \left(a + \frac{a+b}{2}\right) \times h$
ar(ABFE) = $\frac{1}{2} \times \left(\frac{2a + a + b}{2}\right) \times h$
ar(ABFE) = $\frac{1}{2} \times \left(\frac{3a + b}{2}\right) \times h$
ar(ABFE) = $\frac{(3a + b)h}{4}$
... (ii)
Next, we calculate the area of the trapezium EFCD.
ar(EFCD) = $\frac{1}{2} \times (EF + DC) \times h$
Substituting the values of EF and DC:
ar(EFCD) = $\frac{1}{2} \times \left(\frac{a+b}{2} + b\right) \times h$
ar(EFCD) = $\frac{1}{2} \times \left(\frac{a + b + 2b}{2}\right) \times h$
ar(EFCD) = $\frac{1}{2} \times \left(\frac{a + 3b}{2}\right) \times h$
ar(EFCD) = $\frac{(a + 3b)h}{4}$
... (iii)
Finally, we find the ratio of the areas using equations (ii) and (iii):
$\frac{\text{ar(ABFE)}}{\text{ar(EFCD)}} = \frac{\frac{(3a + b)h}{4}}{\frac{(a + 3b)h}{4}}$
Canceling the common term $\frac{h}{4}$ from the numerator and denominator, we get:
$\frac{\text{ar(ABFE)}}{\text{ar(EFCD)}} = \frac{3a + b}{a + 3b}$
Thus, the required ratio is (3a + b) : (a + 3b).
Sample Question 1 & 2 (Before Exercise 9.2)
Write True or False and justify your answer.
Sample Question 1: If P is any point on the median AD of a ∆ ABC, then ar (ABP) ≠ ar (ACP).
Answer:
The given statement is False.
Reason: If P is any point on the median AD of a $\triangle ABC$, then the area of $\triangle ABP$ is always equal to the area of $\triangle ACP$.
Given:
A triangle $\triangle ABC$ where AD is the median to the side BC.
P is any point on the median AD.
To Prove:
ar($\triangle ABP$) = ar($\triangle ACP$)
Proof:
We know that a median of a triangle divides it into two triangles of equal area.
In $\triangle ABC$, AD is the median. Since a median divides the triangle into two triangles of equal areas, we have:
ar($\triangle ABD$) = ar($\triangle ACD$)
... (i)
Now, consider $\triangle PBC$. Since D is the mid-point of BC, PD is the median to the side BC for $\triangle PBC$.
Therefore, PD also divides $\triangle PBC$ into two triangles of equal area.
ar($\triangle PBD$) = ar($\triangle PCD$)
... (ii)
Now, we can find the area of $\triangle ABP$ by subtracting the area of $\triangle PBD$ from the area of $\triangle ABD$.
ar($\triangle ABP$) = ar($\triangle ABD$) - ar($\triangle PBD$)
Similarly, we can find the area of $\triangle ACP$ by subtracting the area of $\triangle PCD$ from the area of $\triangle ACD$.
ar($\triangle ACP$) = ar($\triangle ACD$) - ar($\triangle PCD$)
From equations (i) and (ii), we know that the terms on the right-hand side of the subtraction expressions are equal to each other.
Since ar($\triangle ABD$) = ar($\triangle ACD$) and ar($\triangle PBD$) = ar($\triangle PCD$), it follows that:
ar($\triangle ABD$) - ar($\triangle PBD$) = ar($\triangle ACD$) - ar($\triangle PCD$)
Therefore, ar($\triangle ABP$) = ar($\triangle ACP$).
This contradicts the given statement `ar (ABP) ≠ ar (ACP)`. Hence, the statement is False.
Sample Question 2: If in Fig. 9.7, PQRS and EFRS are two parallelograms, then ar (MFR) = $\frac{1}{2}$ ar (PQRS).

Answer:
The given statement is True.
Reason: Parallelograms on the same base and between the same parallels are equal in area. Then, the area of a triangle is half the area of a parallelogram on the same base and between the same parallels.
Given:
PQRS and EFRS are two parallelograms.
From the figure, they are on the same base SR and between the same parallel lines PF and SR.
M is any point on the side ES.
To Verify:
$ar(\triangle MFR) = \frac{1}{2} ar(PQRS)$
Proof:
We know that parallelograms on the same base and between the same parallels are equal in area.
Here, parallelogram PQRS and parallelogram EFRS are on the same base SR and between the same parallels PF and SR.
Therefore,
ar(PQRS) = ar(EFRS)
... (i)
Now, let's consider $\triangle MFR$ and parallelogram EFRS.
In a parallelogram, opposite sides are parallel. So, in parallelogram EFRS, we have $ES \parallel FR$.
As we can see from the figure, $\triangle MFR$ and parallelogram EFRS are on the same base FR and between the same parallel lines FR and ES (since M is a point on the line segment ES).
We also know that if a triangle and a parallelogram are on the same base and between the same parallels, the area of the triangle is half the area of the parallelogram.
Therefore,
ar($\triangle MFR$) = $\frac{1}{2}$ ar(EFRS)
... (ii)
Using equation (i), we can substitute ar(PQRS) in place of ar(EFRS) in equation (ii).
$ar(\triangle MFR) = \frac{1}{2} ar(PQRS)$
Hence, the given statement is True.
Exercise 9.2
Write True or False and justify your answer :
Question 1. ABCD is a parallelogram and X is the mid-point of AB. If ar (AXCD) = 24 cm2 , then ar (ABC) = 24 cm2 .
Answer:
The given statement is False.
Given:
ABCD is a parallelogram.
X is the mid-point of the side AB.
The area of the trapezium AXCD is 24 cm², i.e., ar(AXCD) = 24 cm².
To Verify:
Whether ar($\triangle ABC$) = 24 cm².
Construction:
Join the diagonal AC.
Proof:
We know that a diagonal of a parallelogram divides it into two triangles of equal area.
Therefore, for parallelogram ABCD with diagonal AC:
ar($\triangle ABC$) = ar($\triangle ADC$) = $\frac{1}{2}$ ar(ABCD)
... (i)
Now, consider $\triangle ABC$. Since X is the mid-point of the side AB, the line segment CX is a median to the side AB.
A median of a triangle divides it into two triangles of equal area. Thus, for $\triangle ABC$:
ar($\triangle AXC$) = ar($\triangle BXC$) = $\frac{1}{2}$ ar($\triangle ABC$)
Let's express ar($\triangle AXC$) in terms of ar(ABCD) using equation (i):
ar($\triangle AXC$) = $\frac{1}{2} \times \left(\frac{1}{2} \text{ ar(ABCD)}\right) = \frac{1}{4}$ ar(ABCD)
... (ii)
From the figure, the area of the trapezium AXCD is the sum of the areas of $\triangle ADC$ and $\triangle AXC$.
ar(AXCD) = ar($\triangle ADC$) + ar($\triangle AXC$)
Substituting the areas from equations (i) and (ii):
ar(AXCD) = $\frac{1}{2}$ ar(ABCD) + $\frac{1}{4}$ ar(ABCD)
ar(AXCD) = $\left(\frac{2+1}{4}\right)$ ar(ABCD) = $\frac{3}{4}$ ar(ABCD)
We are given that ar(AXCD) = 24 cm².
$24 = \frac{3}{4}$ ar(ABCD)
ar(ABCD) = $24 \times \frac{4}{3} = 8 \times 4 = 32$ cm².
Now we find the area of $\triangle ABC$ using equation (i):
ar($\triangle ABC$) = $\frac{1}{2}$ ar(ABCD) = $\frac{1}{2} \times 32 = 16$ cm².
Since 16 cm² is not equal to 24 cm², the given statement is False.
Alternate Solution:
Let the height of the parallelogram with respect to the base AB be $h$.
Area of parallelogram ABCD = Base $\times$ Height = $AB \times h$.
AXCD is a trapezium with parallel sides AX and DC, and height $h$.
We know $DC = AB$ (opposite sides of a parallelogram) and $AX = \frac{1}{2}AB$ (X is the mid-point).
Area of trapezium AXCD = $\frac{1}{2} \times (\text{sum of parallel sides}) \times \text{height}$
ar(AXCD) = $\frac{1}{2} \times (AX + DC) \times h$
ar(AXCD) = $\frac{1}{2} \times \left(\frac{1}{2}AB + AB\right) \times h = \frac{1}{2} \times \left(\frac{3}{2}AB\right) \times h$
ar(AXCD) = $\frac{3}{4} \times (AB \times h) = \frac{3}{4}$ ar(ABCD)
Given ar(AXCD) = 24 cm²:
$24 = \frac{3}{4}$ ar(ABCD)
ar(ABCD) = $32$ cm².
Area of $\triangle ABC$ = $\frac{1}{2}$ ar(ABCD) = $\frac{1}{2} \times 32 = 16$ cm².
This confirms that the statement is false.
Question 2. PQRS is a rectangle inscribed in a quadrant of a circle of radius 13 cm. A is any point on PQ. If PS = 5 cm, then ar (PAS) = 30 cm2 .
Answer:
The given statement is True.
Given:
A rectangle PQRS is inscribed in a quadrant of a circle.
The radius of the circle is 13 cm. In the standard inscription, one vertex (say P) is at the center of the circle, and the opposite vertex (R) lies on the arc. Thus, the diagonal PR is equal to the radius.
So, $PR = 13$ cm.
The length of the side $PS = 5$ cm.
A is any point on PQ.
To Check:
Whether ar($\triangle PAS$) = 30 cm².
Construction:
Solution:
In the rectangle PQRS, the angle at vertex P is $90^\circ$. Let's consider the right-angled triangle $\triangle PSR$.
By the Pythagoras theorem:
$PR^2 = PS^2 + SR^2$
We are given $PR = 13$ cm and $PS = 5$ cm.
$13^2 = 5^2 + SR^2$
$169 = 25 + SR^2$
$SR^2 = 169 - 25 = 144$
$SR = \sqrt{144} = 12$ cm.
Since PQRS is a rectangle, its opposite sides are equal. Therefore, $PQ = SR = 12$ cm.
Now, we need to find the area of $\triangle PAS$. The question states that "A is any point on PQ". For the statement "ar (PAS) = 30 cm²" to be true, we must consider the specific case where the point A coincides with the vertex Q.
If we assume A coincides with Q, then the triangle becomes $\triangle PQS$.
The area of the right-angled triangle $\triangle PQS$ (right-angled at P) is given by:
ar($\triangle PQS$) = $\frac{1}{2} \times \text{base} \times \text{height}$
ar($\triangle PQS$) = $\frac{1}{2} \times PQ \times PS$
Substituting the values we found:
ar($\triangle PQS$) = $\frac{1}{2} \times 12 \times 5$
ar($\triangle PQS$) = $30$ cm².
Under the assumption that the point A in the expression `ar (PAS)` refers to the vertex Q, the statement is correct.
Question 3. PQRS is a parallelogram whose area is 180 cm2 and A is any point on the diagonal QS. The area of ∆ ASR = 90 cm2 .
Answer:
The given statement is False.
Given:
PQRS is a parallelogram.
The area of parallelogram PQRS is 180 cm², i.e., ar(PQRS) = 180 cm².
A is any point on the diagonal QS.
To Check:
Whether the area of $\triangle ASR = 90$ cm².
Construction:
Draw a parallelogram PQRS with diagonal QS. Mark a point A on QS and join it to R and S to form $\triangle ASR$.
Solution:
We know that a diagonal of a parallelogram divides it into two triangles of equal area.
Here, QS is the diagonal of the parallelogram PQRS. Therefore, it divides the parallelogram into two triangles, $\triangle PQS$ and $\triangle RQS$, of equal area.
ar($\triangle RQS$) = $\frac{1}{2} \times$ ar(PQRS)
Substituting the given area of the parallelogram:
ar($\triangle RQS$) = $\frac{1}{2} \times 180 \text{ cm}^2 = 90 \text{ cm}^2$.
Now, consider the triangle $\triangle RQS$. The point A lies on the side QS of this triangle.
The triangle $\triangle ASR$ is a part of the larger triangle $\triangle RQS$. Visually, the area of $\triangle RQS$ is composed of the areas of $\triangle ASR$ and $\triangle AQR$.
ar($\triangle RQS$) = ar($\triangle ASR$) + ar($\triangle AQR$)
$90 \text{ cm}^2$ = ar($\triangle ASR$) + ar($\triangle AQR$)
Since A is "any point" on the diagonal QS, we can assume it is not one of the endpoints Q or S. If A is not the same point as Q, then $\triangle AQR$ is a triangle with a non-zero area.
This means ar($\triangle AQR$) > 0.
Therefore, ar($\triangle ASR$) must be less than 90 cm².
ar($\triangle ASR) < 90 \text{ cm}^2$
The only case where ar($\triangle ASR$) would be equal to 90 cm² is if A coincides with Q, because then $\triangle ASR$ would be the same as $\triangle QSR$. However, the statement implies this is true for *any* point A on the diagonal, which is incorrect.
Hence, the statement that the area of $\triangle ASR = 90$ cm² is False.
Question 4. ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then ar (BDE) = $\frac{1}{4}$ar (ABC).
Answer:
The given statement is True.
Given:
$\triangle ABC$ and $\triangle BDE$ are two equilateral triangles.
D is the mid-point of the side BC of $\triangle ABC$.
To Check:
Whether ar($\triangle BDE$) = $\frac{1}{4}$ ar($\triangle ABC$).
Construction:
An equilateral triangle ABC is drawn. D is the mid-point of BC. Another equilateral triangle BDE is drawn with side BD.
Proof:
Let the side length of the equilateral triangle $\triangle ABC$ be $s$.
So, $AB = BC = CA = s$.
Since D is the mid-point of BC, the length of the segment BD is:
$BD = \frac{1}{2} BC = \frac{s}{2}$.
As $\triangle BDE$ is an equilateral triangle, its side length is equal to the length of BD.
So, side of $\triangle BDE = \frac{s}{2}$.
The formula for the area of an equilateral triangle with side 'a' is $\frac{\sqrt{3}}{4} a^2$.
Area of $\triangle ABC$ is:
ar($\triangle ABC$) = $\frac{\sqrt{3}}{4} (BC)^2 = \frac{\sqrt{3}}{4} s^2$
... (i)
Area of $\triangle BDE$ is:
ar($\triangle BDE$) = $\frac{\sqrt{3}}{4} (BD)^2 = \frac{\sqrt{3}}{4} \left(\frac{s}{2}\right)^2$
ar($\triangle BDE$) = $\frac{\sqrt{3}}{4} \times \frac{s^2}{4}$
ar($\triangle BDE$) = $\frac{1}{4} \left(\frac{\sqrt{3}}{4} s^2\right)$
Substituting the value of ar($\triangle ABC$) from equation (i):
ar($\triangle BDE$) = $\frac{1}{4}$ ar($\triangle ABC$).
Hence, the statement is true.
Alternate Solution (Using Similarity):
Since $\triangle ABC$ and $\triangle BDE$ are both equilateral triangles, all their angles are $60^\circ$.
Therefore, $\triangle ABC$ is similar to $\triangle BDE$ (by AAA similarity criterion).
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
$\frac{\text{ar}(\triangle BDE)}{\text{ar}(\triangle ABC)} = \left(\frac{\text{Side of } \triangle BDE}{\text{Side of } \triangle ABC}\right)^2$
The corresponding sides are BD and BC.
$\frac{\text{ar}(\triangle BDE)}{\text{ar}(\triangle ABC)} = \left(\frac{BD}{BC}\right)^2$
Since D is the mid-point of BC, we have $BD = \frac{1}{2}BC$, which means $\frac{BD}{BC} = \frac{1}{2}$.
$\frac{\text{ar}(\triangle BDE)}{\text{ar}(\triangle ABC)} = \left(\frac{1}{2}\right)^2 = \frac{1}{4}$
Therefore, ar($\triangle BDE$) = $\frac{1}{4}$ ar($\triangle ABC$).
Question 5. In Fig. 9.8, ABCD and EFGD are two parallelograms and G is the mid-point of CD. Then ar (DPC) = $\frac{1}{2}$ ar ( EFGD)

Answer:
The given statement is False.
Given:
ABCD and EFGD are two parallelograms.
From the figure, they are between the same parallel lines AB and DC.
G is the mid-point of the side CD.
P is a point on the line segment AB.
To Check:
Whether ar($\triangle DPC$) = $\frac{1}{2}$ ar(EFGD).
Proof:
First, let's relate the area of $\triangle DPC$ to the area of parallelogram ABCD.
The triangle $\triangle DPC$ and the parallelogram ABCD lie on the same base DC and are between the same parallel lines AB and DC.
According to the theorem, the area of a triangle is half the area of a parallelogram on the same base and between the same parallels.
ar($\triangle DPC$) = $\frac{1}{2}$ ar(ABCD)
... (i)
Next, let's relate the area of parallelogram EFGD to the area of parallelogram ABCD.
Let $h$ be the perpendicular distance (height) between the parallel lines AB and DC.
Area of a parallelogram = Base $\times$ Height.
ar(ABCD) = $DC \times h$
ar(EFGD) = $DG \times h$
We are given that G is the mid-point of CD, which means:
$DG = \frac{1}{2} DC$
Now, substitute this into the area formula for EFGD:
ar(EFGD) = $\left(\frac{1}{2} DC\right) \times h = \frac{1}{2} (DC \times h)$
Since ar(ABCD) = $DC \times h$, we can write:
ar(EFGD) = $\frac{1}{2}$ ar(ABCD)
... (ii)
From equations (i) and (ii), we can see that both ar($\triangle DPC$) and ar(EFGD) are equal to half the area of parallelogram ABCD.
Therefore,
ar($\triangle DPC$) = ar(EFGD)
Since ar($\triangle DPC$) is equal to ar(EFGD), the statement that ar($\triangle DPC$) = $\frac{1}{2}$ ar(EFGD) is False.
Sample Question 1 & 2 (Before Exercise 9.3)
Sample Question 1: PQRS is a square. T and U are respectively, the mid-points of PS and QR (Fig. 9.9). Find the area of ∆ OTS, if PQ = 8 cm, where O is the point of intersection of TU and QS
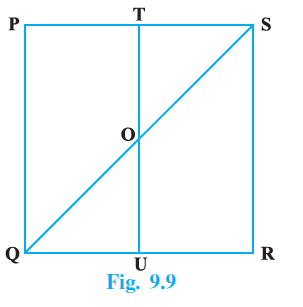
Answer:
Given:
PQRS is a square.
The side length of the square, $PQ = 8$ cm.
T is the mid-point of the side PS.
U is the mid-point of the side QR.
O is the point of intersection of the line segment TU and the diagonal QS.
To Find:
The area of $\triangle OTS$.
Solution:
Since PQRS is a square and $PQ = 8$ cm, all its sides are 8 cm long.
$PQ = QR = RS = PS = 8$ cm.
T is the mid-point of the side PS. Therefore, the length of ST is:
$ST = \frac{1}{2} \times PS = \frac{1}{2} \times 8 = 4$ cm.
The line segment TU joins the mid-points of the opposite sides PS and QR of the square. Therefore, TU is parallel to the sides PQ and SR, and its length is equal to the side of the square.
$TU \parallel PQ$ and $TU = PQ = 8$ cm.
In a square, adjacent sides are perpendicular to each other. So, $PS \perp PQ$.
This means the angle $\angle SPQ = 90^\circ$.
Since we have established that $TU \parallel PQ$ and $PS \perp PQ$, it follows that TU must also be perpendicular to PS.
$PS \perp TU$.
Therefore, the angle $\angle OTS = 90^\circ$. This means that $\triangle OTS$ is a right-angled triangle.
Now, we need to find the length of the side OT. Consider the triangles $\triangle SOT$ and $\triangle QOU$.
$ST = QU$
(Halves of equal sides PS and QR)
$\angle TSO = \angle UQO$
(Alternate interior angles as $PS \parallel QR$)
$\angle STO = \angle QUO$
(Both are $90^\circ$)
By Angle-Angle-Side (AAS) congruence, $\triangle SOT \cong \triangle QOU$.
By CPCTC (Corresponding Parts of Congruent Triangles are Congruent), $OT = OU$.
This shows that O is the mid-point of TU.
So, $OT = \frac{1}{2} \times TU = \frac{1}{2} \times 8 = 4$ cm.
Now we can find the area of the right-angled triangle $\triangle OTS$.
Area($\triangle OTS$) = $\frac{1}{2} \times \text{base} \times \text{height}$
Area($\triangle OTS$) = $\frac{1}{2} \times ST \times OT$
Area($\triangle OTS$) = $\frac{1}{2} \times 4 \text{ cm} \times 4 \text{ cm}$
Area($\triangle OTS$) = $8 \text{ cm}^2$.
Hence, the area of $\triangle OTS$ is 8 cm2.
Sample Question 2: ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ (Fig. 9.10). If AQ intersects DC at P, show that ar (BPC) = ar (DPQ).
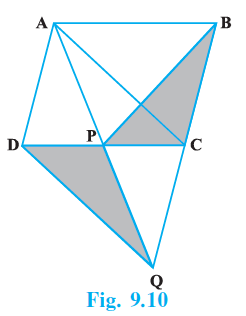
Answer:
Given:
ABCD is a parallelogram.
The side BC is produced to a point Q such that $AD = CQ$.
The line segment AQ intersects the side DC at point P.
To Prove:
ar($\triangle BPC$) = ar($\triangle DPQ$).
Proof:
Since ABCD is a parallelogram, its opposite sides are equal and parallel.
$AD = BC$
(Opposite sides of a parallelogram)
$AD \parallel BC$
(Opposite sides of a parallelogram)
We are given that:
$AD = CQ$
(Given)
From the above equations, we can conclude that:
$BC = CQ$
This means that C is the mid-point of the line segment BQ.
Now, let's compare the triangles $\triangle APD$ and $\triangle QPC$.
Since $AD \parallel BC$, and BC is extended to Q, we have $AD \parallel BQ$.
$\angle PAD = \angle PQC$
(Alternate interior angles)
$\angle APD = \angle QPC$
(Vertically opposite angles)
$AD = CQ$
(Given)
By the Angle-Angle-Side (AAS) congruence rule, we have:
$\triangle APD \cong \triangle QPC$
Since the triangles are congruent, their corresponding parts are equal. Therefore:
$DP = CP$
This shows that P is the mid-point of the side DC.
Also, the areas of congruent triangles are equal:
ar($\triangle APD$) = ar($\triangle QPC$)
Now, consider $\triangle BQD$.
Since C is the mid-point of BQ and P is the mid-point of DC, the line segment PC connects the mid-points of two sides of the triangle.
By the Mid-point Theorem, $PC \parallel BD$ and $PC = \frac{1}{2} BD$.
Let's consider $\triangle BPC$ and $\triangle DPQ$.
In $\triangle BDQ$, P is the mid-point of DC and C is the mid-point of BQ. PC is a line segment connecting these points.
Also, in $\triangle ACQ$, P is the mid-point of DC. It is also the mid-point of AQ because of the congruence $\triangle APD \cong \triangle QPC$ which implies $AP=QP$.
Let's use a simpler approach based on medians.
In $\triangle PBQ$, since C is the mid-point of BQ, PC is a median.
A median divides a triangle into two triangles of equal area. Therefore,
ar($\triangle BPC$) = ar($\triangle PQC$)
... (i)
Now consider $\triangle DQC$. Since P is the mid-point of DC, QP is a median.
Therefore, QP divides $\triangle DQC$ into two triangles of equal area.
ar($\triangle DPQ$) = ar($\triangle CPQ$)
... (ii)
From equations (i) and (ii), we can see that both ar($\triangle BPC$) and ar($\triangle DPQ$) are equal to ar($\triangle PQC$).
ar($\triangle BPC$) = ar($\triangle DPQ$)
Hence, Proved.
Exercise 9.3
Question 1. In Fig.9.11, PSDA is a parallelogram. Points Q and R are taken on PS such that PQ = QR = RS and PA || QB || RC. Prove that ar (PQE) = ar (CFD).
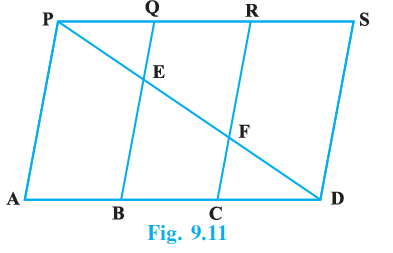
Answer:
Given:
PSDA is a parallelogram, which means $PS \parallel AD$ and $PA \parallel SD$.
Points Q and R are on the side PS such that $PQ = QR = RS$.
It is also given that $PA \parallel QB \parallel RC$.
To Prove:
ar ($\triangle PQE$) = ar ($\triangle CFD$).
Proof:
First, we will establish the relationships between the various line segments using the Intercept Theorem.
We have a set of parallel lines: $PA \parallel QB \parallel RC$. Since $PA \parallel SD$ (from parallelogram PSDA), we can say that all four lines are parallel to each other: $PA \parallel QB \parallel RC \parallel SD$.
These parallel lines are intersected by two transversals, PS and AD.
According to the Intercept Theorem, if a transversal makes equal intercepts on three or more parallel lines, then any other transversal will also make equal intercepts.
The transversal PS makes equal intercepts, as given:
$PQ = QR = RS$
(Given)
Therefore, the intercepts made by these parallel lines on the transversal AD must also be equal.
$AB = BC = CD$
... (i)
Since RCDS is a quadrilateral with $RS \parallel CD$ (parts of parallel lines PS and AD) and $RC \parallel SD$ (given $RC \parallel PA$ and $PA \parallel SD$), RCDS is a parallelogram. Thus, $RS = CD$.
As $PQ = RS$, we have:
$PQ = CD$
... (ii)
Now, let's consider the transversal PD. The parallel lines $PA, QB, RC, SD$ also cut the transversal PD at points P, E, F, and D respectively. Since the intercepts on transversal PS are equal, the intercepts on transversal PD must also be equal.
$PE = EF = FD$
... (iii)
Now we will prove the congruence of $\triangle PQE$ and $\triangle DFC$ (which is the same as $\triangle CFD$).
In $\triangle PQE$ and $\triangle DFC$:
$PQ = DC$
[From (ii)]
$PE = DF$
[From (iii)]
Since PSDA is a parallelogram, $PS \parallel AD$. Considering PD as a transversal, the alternate interior angles are equal.
$\angle SPD = \angle PDA$
(Alternate interior angles)
This can be written as:
$\angle QPE = \angle FDC$
So, by the Side-Angle-Side (SAS) congruence criterion:
$\triangle PQE \cong \triangle DFC$
We know that congruent triangles have equal areas.
Therefore, ar ($\triangle PQE$) = ar ($\triangle DFC$)
or, ar ($\triangle PQE$) = ar ($\triangle CFD$).
Hence, Proved.
Question 2. X and Y are points on the side LN of the triangle LMN such that LX = XY = YN. Through X, a line is drawn parallel to LM to meet MN at Z (See Fig. 9.12). Prove that ar (LZY) = ar (MZYX)

Answer:
Given:
In $\triangle LMN$, X and Y are points on the side LN such that $LX = XY = YN$.
A line is drawn through X parallel to LM, meeting MN at Z. So, $XZ \parallel LM$.
To Prove:
ar (LZY) = ar (MZYX).
Proof:
We are given that $XZ \parallel LM$.
Consider the triangles $\triangle XLZ$ and $\triangle XMZ$.
These two triangles lie on the same base XZ.
They also lie between the same parallel lines LM and XZ, since their vertices L and M lie on the line LM which is parallel to the base XZ.
According to the theorem, triangles on the same base and between the same parallels are equal in area.
Therefore, we can write:
ar($\triangle XLZ$) = ar($\triangle XMZ$)
... (i)
Now, let's add the area of $\triangle XYZ$ to both sides of equation (i).
ar($\triangle XLZ$) + ar($\triangle XYZ$) = ar($\triangle XMZ$) + ar($\triangle XYZ$)
From the figure, we can see that:
ar($\triangle XLZ$) + ar($\triangle XYZ$) = ar($\triangle LZY$)
and
ar($\triangle XMZ$) + ar($\triangle XYZ$) = ar(quadrilateral MZYX)
Substituting these back into our equation, we get:
ar($\triangle LZY$) = ar(MZYX)
Hence, Proved.
Note: The condition that LX = XY = YN is extra information and is not required for this particular proof.
Question 3. The area of the parallelogram ABCD is 90 cm2 (see Fig.9.13). Find
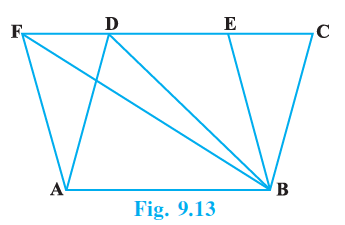
(i) ar (ABEF)
(ii) ar (ABD)
(iii) ar (BEF)
Answer:
Given:
The area of the parallelogram ABCD is 90 cm².
From the figure, ABCD and ABEF are two parallelograms on the same base AB and between the same parallel lines AB and FC.
To Find:
(i) ar (ABEF)
(ii) ar ($\triangle$ABD)
(iii) ar ($\triangle$BEF)
Solution:
(i) To find ar (ABEF)
We know the theorem that states: Parallelograms on the same base and between the same parallels are equal in area.
Here, parallelogram ABCD and parallelogram ABEF are on the same base AB and lie between the same parallel lines AB and FC.
Therefore, ar (ABEF) = ar (ABCD).
Since it is given that ar (ABCD) = 90 cm²,
ar (ABEF) = 90 cm².
(ii) To find ar ($\triangle$ABD)
We know the theorem that states: If a triangle and a parallelogram are on the same base and between the same parallels, then the area of the triangle is half the area of the parallelogram.
Here, $\triangle$ABD and parallelogram ABCD are on the same base AB and between the same parallel lines AB and DC.
Therefore, ar ($\triangle$ABD) = $\frac{1}{2}$ ar (ABCD).
Substituting the given area:
ar ($\triangle$ABD) = $\frac{1}{2} \times 90$ cm²
ar ($\triangle$ABD) = 45 cm².
(Alternatively, the diagonal BD divides the parallelogram ABCD into two triangles of equal area.)
(iii) To find ar ($\triangle$BEF)
Using the same theorem as in part (ii), we consider $\triangle$BEF and parallelogram ABEF.
Here, $\triangle$BEF and parallelogram ABEF are on the same base EF and between the same parallel lines EF and AB.
Therefore, ar ($\triangle$BEF) = $\frac{1}{2}$ ar (ABEF).
From the result of part (i), we know that ar (ABEF) = 90 cm².
ar ($\triangle$BEF) = $\frac{1}{2} \times 90$ cm²
ar ($\triangle$BEF) = 45 cm².
(Alternatively, the diagonal BF divides the parallelogram ABEF into two triangles of equal area, so ar ($\triangle$BEF) is half the area of the parallelogram.)
Question 4. In ∆ ABC, D is the mid-point of AB and P is any point on BC. If CQ || PD meets AB in Q (Fig. 9.14), then prove that ar (BPQ) = $\frac{1}{2}$ ar (ABC).
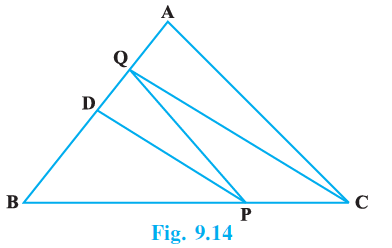
Answer:
Given:
In $\triangle ABC$, D is the mid-point of the side AB.
P is any point on the side BC.
A line segment CQ is drawn such that it is parallel to PD and it meets the side AB at point Q. So, $CQ \parallel PD$.
To Prove:
ar ($\triangle BPQ$) = $\frac{1}{2}$ ar ($\triangle ABC$).
Construction:
Join the points C and D to form the line segment CD.
Proof:
Since D is the mid-point of the side AB in $\triangle ABC$, the line segment CD is a median of the triangle.
We know that a median of a triangle divides it into two triangles of equal area.
Therefore,
ar ($\triangle BCD$) = $\frac{1}{2}$ ar ($\triangle ABC$)
... (i)
Now, consider the triangles $\triangle PDQ$ and $\triangle PDC$.
These two triangles lie on the same base PD.
They are also between the same parallel lines PD and CQ (as given that $CQ \parallel PD$).
According to the theorem, triangles on the same base and between the same parallels are equal in area.
So, we have:
ar ($\triangle PDQ$) = ar ($\triangle PDC$)
... (ii)
From the figure, we can express the area of $\triangle BCD$ as the sum of the areas of two smaller triangles:
ar ($\triangle BCD$) = ar ($\triangle BPD$) + ar ($\triangle PDC$)
Substituting the value from equation (i):
ar ($\triangle BPD$) + ar ($\triangle PDC$) = $\frac{1}{2}$ ar ($\triangle ABC$)
Now, using equation (ii), we can replace ar ($\triangle PDC$) with ar ($\triangle PDQ$):
ar ($\triangle BPD$) + ar ($\triangle PDQ$) = $\frac{1}{2}$ ar ($\triangle ABC$)
Again, from the figure, the sum of the areas of $\triangle BPD$ and $\triangle PDQ$ is equal to the area of $\triangle BPQ$.
ar ($\triangle BPQ$) = ar ($\triangle BPD$) + ar ($\triangle PDQ$)
Therefore, we can conclude that:
ar ($\triangle BPQ$) = $\frac{1}{2}$ ar ($\triangle ABC$)
Hence, Proved.
Question 5. ABCD is a square. E and F are respectively the midpoints of BC and CD. If R is the mid-point of EF (Fig. 9.15), prove that ar (AER) = ar (AFR)
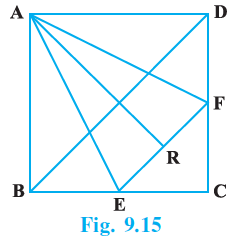
Answer:
Given:
ABCD is a square.
E is the mid-point of the side BC.
F is the mid-point of the side CD.
R is the mid-point of the line segment EF.
To Prove:
ar ($\triangle$AER) = ar ($\triangle$AFR).
Proof:
Consider the triangle $\triangle AEF$.
We are given that R is the mid-point of the side EF.
A line segment joining a vertex of a triangle to the mid-point of its opposite side is called a median.
Therefore, AR is the median of $\triangle AEF$ to the side EF.
We know that a median of a triangle divides it into two triangles of equal area.
Since AR is the median of $\triangle AEF$, it divides the triangle into two triangles, $\triangle AER$ and $\triangle AFR$, of equal areas.
Therefore, ar($\triangle$AER) = ar($\triangle$AFR).
Hence, Proved.
Question 6. O is any point on the diagonal PR of a parallelogram PQRS (Fig. 9.16). Prove that ar (PSO) = ar (PQO).
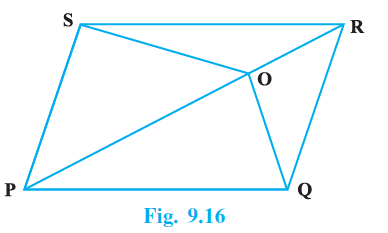
Answer:
Given:
A parallelogram PQRS.
O is any point on the diagonal PR.
To Prove:
ar ($\triangle$PSO) = ar ($\triangle$PQO).
Construction:
Join the diagonal SQ, which intersects the diagonal PR at point B.
Proof:
We know that the diagonals of a parallelogram bisect each other. Therefore, the point of intersection B is the mid-point of the diagonal SQ.
Now, consider the triangle $\triangle QPS$. Since B is the mid-point of the side SQ, the line segment PB is a median of $\triangle QPS$.
A median of a triangle divides it into two triangles of equal area. Therefore,
ar ($\triangle$BPQ) = ar ($\triangle$BPS)
... (i)
Similarly, consider the triangle $\triangle OSQ$. Since B is the mid-point of the side SQ, the line segment OB is a median of $\triangle OSQ$.
Therefore,
ar ($\triangle$OBQ) = ar ($\triangle$OBS)
... (ii)
The point O can lie either between P and B, or between B and R. We will consider both cases.
Case 1: O lies between B and R.
In this case, ar ($\triangle$PQO) = ar ($\triangle$BPQ) + ar ($\triangle$OBQ) and ar ($\triangle$PSO) = ar ($\triangle$BPS) + ar ($\triangle$OBS).
On adding equation (i) and equation (ii), we get:
ar ($\triangle$BPQ) + ar ($\triangle$OBQ) = ar ($\triangle$BPS) + ar ($\triangle$OBS)
Therefore, ar ($\triangle$PQO) = ar ($\triangle$PSO).
Case 2: O lies between P and B.
In this case, ar ($\triangle$PQO) = ar ($\triangle$BPQ) - ar ($\triangle$OBQ) and ar ($\triangle$PSO) = ar ($\triangle$BPS) - ar ($\triangle$OBS).
On subtracting equation (ii) from equation (i), we get:
ar ($\triangle$BPQ) - ar ($\triangle$OBQ) = ar ($\triangle$BPS) - ar ($\triangle$OBS)
Therefore, ar ($\triangle$PQO) = ar ($\triangle$PSO).
In both cases, the result holds true.
ar ($\triangle$PSO) = ar ($\triangle$PQO)
Hence, Proved.
Question 7. ABCD is a parallelogram in which BC is produced to E such that CE = BC (Fig. 9.17). AE intersects CD at F.
If ar (DFB) = 3 cm2 , find the area of the parallelogram ABCD.

Answer:
Given:
ABCD is a parallelogram.
The side BC is produced to a point E such that $BC = CE$.
The line segment AE intersects the side CD at point F.
The area of $\triangle DFB$ is 3 cm², i.e., ar($\triangle DFB$) = 3 cm².
To Find:
The area of the parallelogram ABCD.
Solution:
Since ABCD is a parallelogram, its opposite sides are parallel and equal.
$AD \parallel BC$ (and thus $AD \parallel BE$)
$AD = BC$
(Opposite sides of a parallelogram)
We are also given that:
$BC = CE$
(Given)
From the above two equations, we get:
$AD = CE$
... (i)
Now, let's consider the triangles $\triangle ADF$ and $\triangle ECF$.
$\angle DAF = \angle CEF$
(Alternate interior angles, as $AD \parallel BE$ and AE is the transversal)
$\angle AFD = \angle EFC$
(Vertically opposite angles)
$AD = CE$
[From equation (i)]
By the Angle-Angle-Side (AAS) congruence rule, we have:
$\triangle ADF \cong \triangle ECF$
Since the triangles are congruent, their corresponding sides are equal. Therefore:
$DF = CF$
This means that F is the mid-point of the side CD.
Now, consider the triangle $\triangle BCD$. Since F is the mid-point of the side CD, the line segment BF is a median of $\triangle BCD$.
We know that a median of a triangle divides it into two triangles of equal area.
Therefore,
ar($\triangle BDF$) = ar($\triangle BCF$)
We are given that ar($\triangle DFB$) = 3 cm². So,
ar($\triangle BCF$) = 3 cm².
The area of $\triangle BCD$ is the sum of the areas of these two triangles:
ar($\triangle BCD$) = ar($\triangle BDF$) + ar($\triangle BCF$)
ar($\triangle BCD$) = 3 cm² + 3 cm² = 6 cm².
Finally, we know that a diagonal of a parallelogram divides it into two triangles of equal area. The diagonal BD divides parallelogram ABCD into $\triangle ABD$ and $\triangle BCD$.
ar(ABCD) = 2 $\times$ ar($\triangle BCD$)
ar(ABCD) = 2 $\times$ 6 cm²
ar(ABCD) = 12 cm².
Hence, the area of the parallelogram ABCD is 12 cm².
Question 8. In trapezium ABCD, AB || DC and L is the mid-point of BC. Through L, a line PQ || AD has been drawn which meets AB in P and DC produced in Q (Fig. 9.18). Prove that ar (ABCD) = ar (APQD).
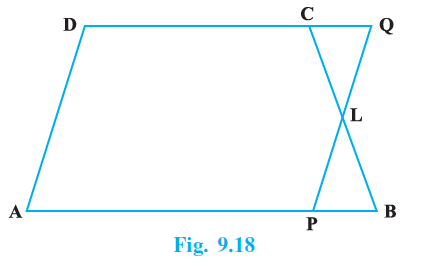
Answer:
Given:
A trapezium ABCD with parallel sides $AB \parallel DC$.
L is the mid-point of the side BC, which means $BL = LC$.
A line PQ is drawn through L parallel to AD. The line meets AB at P and the extension of DC at Q.
To Prove:
ar (ABCD) = ar (APQD).
Proof:
Our strategy is to show that the area of the triangle removed from the quadrilateral APQD to form the trapezium ABCD is equal to the area of the triangle added to it.
Let's compare the triangles $\triangle BLP$ and $\triangle CLQ$.
In $\triangle BLP$ and $\triangle CLQ$:
$\angle BLP = \angle CLQ$
(Vertically opposite angles)
$BL = CL$
(Given that L is the mid-point of BC)
Since $AB \parallel DC$, it follows that the line AB is parallel to the line containing DQ. Considering PQ as a transversal:
$\angle BPL = \angle CQL$
(Alternate interior angles)
By the Angle-Angle-Side (AAS) congruence rule, we have:
$\triangle BLP \cong \triangle CLQ$
Since congruent triangles have equal areas, we can say:
ar ($\triangle$BLP) = ar ($\triangle$CLQ)
... (i)
Let's consider the area of pentagon APLCD.
ar (ABCD) = ar (APLCD) + ar ($\triangle$PBL)
ar (APQD) = ar (APLCD) + ar ($\triangle$LCQ)
Since we proved in equation (i) that ar ($\triangle$PBL) = ar ($\triangle$LCQ), it follows that the right-hand sides of the above two expressions are equal.
Therefore, ar (ABCD) = ar (APQD).
Hence, Proved.
Question 9. If the mid-points of the sides of a quadrilateral are joined in order, prove that the area of the parallelogram so formed will be half of the area of the given quadrilateral (Fig. 9.19).
[Hint: Join BD and draw perpendicular from A on BD.]

Answer:
Given:
A quadrilateral ABCD.
S, P, F, and R are the mid-points of the sides AB, BC, CD, and DA respectively. The mid-points are joined in order to form a quadrilateral SPFR.
To Prove:
The area of the parallelogram SPFR is half the area of the quadrilateral ABCD.
ar (SPFR) = $\frac{1}{2}$ ar (ABCD).
Construction:
Join the diagonal AC of the quadrilateral ABCD.
Proof:
First, we will prove that SPFR is a parallelogram.
In $\triangle ABC$, S and P are the mid-points of sides AB and BC respectively.
By the Mid-point Theorem, the line segment joining the mid-points of two sides of a triangle is parallel to the third side and is half of its length.
$SP \parallel AC$ and $SP = \frac{1}{2} AC$
... (i)
Similarly, in $\triangle ADC$, R and F are the mid-points of sides DA and DC respectively.
By the Mid-point Theorem:
$RF \parallel AC$ and $RF = \frac{1}{2} AC$
... (ii)
From equations (i) and (ii), we can see that:
$SP \parallel RF$ and $SP = RF$
Since one pair of opposite sides of the quadrilateral SPFR is equal and parallel, SPFR is a parallelogram.
Now, we will prove the relationship between the areas.
The area of the parallelogram SPFR can be found by subtracting the areas of the four corner triangles ($\triangle$SAR, $\triangle$SBP, $\triangle$PCF, $\triangle$RDF) from the area of the quadrilateral ABCD.
ar(SPFR) = ar(ABCD) - (ar($\triangle$SAR) + ar($\triangle$SBP) + ar($\triangle$PCF) + ar($\triangle$RDF))
We know that a line segment joining the mid-points of two sides of a triangle divides it into a smaller triangle and a trapezium, and the area of the smaller triangle is one-fourth the area of the original triangle.
In $\triangle ABC$, S and P are mid-points of AB and BC. So, ar($\triangle$SBP) = $\frac{1}{4}$ ar($\triangle$ABC).
In $\triangle ADC$, R and F are mid-points of AD and DC. So, ar($\triangle$RDF) = $\frac{1}{4}$ ar($\triangle$ADC).
Adding these two results:
ar($\triangle$SBP) + ar($\triangle$RDF) = $\frac{1}{4}$ ar($\triangle$ABC) + $\frac{1}{4}$ ar($\triangle$ADC)
ar($\triangle$SBP) + ar($\triangle$RDF) = $\frac{1}{4}$ [ar($\triangle$ABC) + ar($\triangle$ADC)]
ar($\triangle$SBP) + ar($\triangle$RDF) = $\frac{1}{4}$ ar (ABCD)
... (iii)
Similarly, by considering the diagonal BD, we can find the areas of the other two corner triangles.
In $\triangle ABD$, S and R are mid-points of AB and AD. So, ar($\triangle$SAR) = $\frac{1}{4}$ ar($\triangle$ABD).
In $\triangle BCD$, P and F are mid-points of BC and CD. So, ar($\triangle$PCF) = $\frac{1}{4}$ ar($\triangle$BCD).
Adding these two results:
ar($\triangle$SAR) + ar($\triangle$PCF) = $\frac{1}{4}$ ar($\triangle$ABD) + $\frac{1}{4}$ ar($\triangle$BCD)
ar($\triangle$SAR) + ar($\triangle$PCF) = $\frac{1}{4}$ [ar($\triangle$ABD) + ar($\triangle$BCD)]
ar($\triangle$SAR) + ar($\triangle$PCF) = $\frac{1}{4}$ ar (ABCD)
... (iv)
The total area of the four corner triangles is the sum of results from (iii) and (iv):
Area(corner triangles) = (ar($\triangle$SBP) + ar($\triangle$RDF)) + (ar($\triangle$SAR) + ar($\triangle$PCF))
Area(corner triangles) = $\frac{1}{4}$ ar(ABCD) + $\frac{1}{4}$ ar(ABCD) = $\frac{1}{2}$ ar(ABCD)
Now, we find the area of the parallelogram SPFR:
ar(SPFR) = ar(ABCD) - Area(corner triangles)
ar(SPFR) = ar(ABCD) - $\frac{1}{2}$ ar(ABCD)
ar(SPFR) = $\frac{1}{2}$ ar(ABCD)
Hence, Proved.
Sample Question 1 to 3 (Before Exercise 9.4)
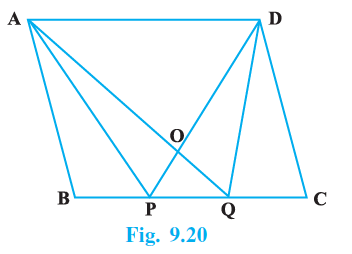
Sample Question 1: In Fig. 9.20, ABCD is a parallelogram. Points P and Q on BC trisects BC in three equal parts. Prove that ar (APQ) = ar (DPQ) = $\frac{1}{6}$ ar(ABCD)
Answer:
Given:
ABCD is a parallelogram.
Points P and Q are on the side BC such that they trisect it. This means $BP = PQ = QC$.
To Prove:
ar ($\triangle$APQ) = ar ($\triangle$DPQ) = $\frac{1}{6}$ ar(ABCD).
Construction:
Draw a line segment from vertex A perpendicular to the side BC, and let it meet BC at M. Let the length of this perpendicular be $h$. This is the height of the parallelogram ABCD corresponding to the base BC.
Proof:
The area of a triangle is given by the formula: Area = $\frac{1}{2} \times \text{base} \times \text{height}$.
The area of a parallelogram is given by the formula: Area = base $\times$ height.
First, we will prove that ar ($\triangle$APQ) = ar ($\triangle$DPQ).
Consider the triangles $\triangle APQ$ and $\triangle DPQ$. They both lie on the same base PQ.
Since ABCD is a parallelogram, we have $AD \parallel BC$.
The height of $\triangle APQ$ from vertex A to the base PQ is the perpendicular distance from A to the line BC, which is $h$.
The height of $\triangle DPQ$ from vertex D to the base PQ is the perpendicular distance from D to the line BC, which is also $h$, because the distance between two parallel lines is constant.
Area ($\triangle APQ$) = $\frac{1}{2} \times PQ \times h$.
Area ($\triangle DPQ$) = $\frac{1}{2} \times PQ \times h$.
Since both areas are equal to the same expression, we have:
ar ($\triangle$APQ) = ar ($\triangle$DPQ)
... (i)
Next, we will prove that ar ($\triangle$APQ) = $\frac{1}{6}$ ar(ABCD).
The area of parallelogram ABCD with base BC and height $h$ is:
ar(ABCD) = $BC \times h$
... (ii)
The area of $\triangle APQ$ with base PQ and height $h$ is:
ar ($\triangle$APQ) = $\frac{1}{2} \times PQ \times h$
... (iii)
We are given that P and Q trisect the side BC. This means:
$BC = BP + PQ + QC$
Since $BP = PQ = QC$, we can write:
$BC = PQ + PQ + PQ = 3 \times PQ$
Or, $PQ = \frac{1}{3} BC$.
Now, substitute this relation into the area formula for $\triangle APQ$ (equation iii):
ar ($\triangle$APQ) = $\frac{1}{2} \times \left(\frac{1}{3} BC\right) \times h$
ar ($\triangle$APQ) = $\frac{1}{6} \times (BC \times h)$
Using equation (ii), we can replace $(BC \times h)$ with ar(ABCD):
ar ($\triangle$APQ) = $\frac{1}{6}$ ar(ABCD)
... (iv)
From equations (i) and (iv), we can combine the results:
ar ($\triangle$APQ) = ar ($\triangle$DPQ) = $\frac{1}{6}$ ar(ABCD)
Hence, Proved.
Sample Question 2: In Fig. 9.22, l, m, n, are straight lines such that l || m and n intersects l at P and m at Q. BCD is a quadrilateral such that its vertex A is on l. The vertices C and D are on m and AD || n. Show that ar (ABCQ) = ar (ABCDP).

Answer:
Given:
l, m, n are straight lines such that $l \parallel m$.
The line n intersects line l at P and line m at Q.
ABCD is a quadrilateral with vertex A on line l, and vertices C and D on line m.
It is also given that the side $AD \parallel n$.
To Prove:
ar (ABCQ) = ar (ABCDP).
Proof:
Consider the triangles $\triangle APD$ and $\triangle AQD$.
These two triangles lie on the same base AD.
They also lie between the same parallel lines, AD and n (which contains the line segment PQ), because it is given that $AD \parallel n$.
We know that triangles on the same base and between the same parallels are equal in area.
Therefore,
ar($\triangle APD$) = ar($\triangle AQD$)
... (i)
Now, adding the area of quadrilateral ABCD to both sides of equation (i), we get:
ar (ABCD) + ar($\triangle APD$) = ar (ABCD) + ar($\triangle AQD$)
From the figure, we can observe that:
ar (ABCD) + ar($\triangle APD$) = ar (pentagon ABCDP)
And,
ar (ABCD) + ar($\triangle AQD$) = ar (quadrilateral ABCQ)
So, the equation becomes:
ar (ABCDP) = ar (ABCQ)
Hence, Proved.
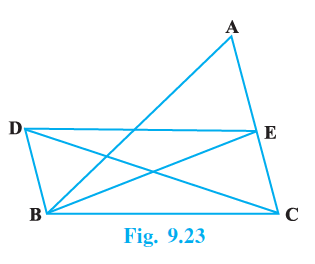
Sample Questions 3: In Fig. 9.23, BD || CA, E is mid-point of CA and BD = $\frac{1}{2}$ CA. Prove that ar(ABC) = 2 ar(DBC)
Answer:
Given:
In the given figure, we have:
$BD \parallel CA$.
E is the mid-point of the side CA, which implies $AE = EC = \frac{1}{2} CA$.
$BD = \frac{1}{2} CA$.
To Prove:
ar($\triangle$ABC) = 2 ar($\triangle$DBC).
Proof:
We are given that E is the mid-point of CA. Therefore,
$CE = \frac{1}{2} CA$
... (i)
It is also given that:
$BD = \frac{1}{2} CA$
... (ii)
From equations (i) and (ii), we can conclude that:
$BD = CE$
... (iii)
We are given that $BD \parallel CA$. Since E is a point on the line segment CA, it follows that:
$BD \parallel CE$
... (iv)
From (iii) and (iv), in the quadrilateral BCED, one pair of opposite sides (BD and CE) is both equal and parallel. Therefore, BCED is a parallelogram.
Now, consider $\triangle DBC$ and $\triangle EBC$.
These two triangles lie on the same base BC.
Since BCED is a parallelogram, its opposite sides are parallel, so $DE \parallel BC$.
Thus, $\triangle DBC$ and $\triangle EBC$ are on the same base BC and between the same parallel lines BC and DE.
We know that triangles on the same base and between the same parallels are equal in area.
ar($\triangle$DBC) = ar($\triangle$EBC)
... (v)
Now, let's consider the original triangle, $\triangle ABC$.
Since E is the mid-point of the side CA, the line segment BE is a median of $\triangle ABC$.
A median of a triangle divides it into two triangles of equal area.
Therefore, ar($\triangle$EBC) = $\frac{1}{2}$ ar($\triangle$ABC).
ar($\triangle$EBC) = $\frac{1}{2}$ ar($\triangle$ABC)
... (vi)
Using the results from equation (v) and equation (vi), we can substitute ar($\triangle$DBC) for ar($\triangle$EBC) in equation (vi).
ar($\triangle$DBC) = $\frac{1}{2}$ ar($\triangle$ABC)
Multiplying both sides by 2, we get:
2 ar($\triangle$DBC) = ar($\triangle$ABC)
Hence, Proved.
Exercise 9.4
Question 1. A point E is taken on the side BC of a parallelogram ABCD. AE and DC are produced to meet at F. Prove that ar (ADF) = ar (ABFC).
Answer:
Given:
ABCD is a parallelogram.
A point E is taken on the side BC.
The line segment AE is produced to meet the line DC (which is also produced) at point F.
To Prove:
ar (ADF) = ar (ABFC).
Construction:
Join the points A and C to form the diagonal AC.
Proof:
Consider the area of the quadrilateral ABFC. It can be expressed as the sum of the areas of two triangles, $\triangle ABC$ and $\triangle ACF$.
ar (ABFC) = ar ($\triangle$ABC) + ar ($\triangle$ACF)
... (i)
Now, consider the area of the triangle $\triangle ADF$. Since C is a point on the side DF, the area of $\triangle ADF$ can be expressed as the sum of the areas of two triangles, $\triangle ADC$ and $\triangle ACF$.
ar ($\triangle$ADF) = ar ($\triangle$ADC) + ar ($\triangle$ACF)
... (ii)
We know that a diagonal of a parallelogram divides it into two triangles of equal area. In parallelogram ABCD, AC is a diagonal.
Therefore,
ar ($\triangle$ABC) = ar ($\triangle$ADC)
... (iii)
Comparing equations (i) and (ii), we can see that the term `ar ($\triangle$ACF)` is common to both expressions.
From equation (iii), we know that the other terms, `ar ($\triangle$ABC)` and `ar ($\triangle$ADC)`, are equal.
Therefore, the right-hand sides of equations (i) and (ii) are equal.
ar ($\triangle$ABC) + ar ($\triangle$ACF) = ar ($\triangle$ADC) + ar ($\triangle$ACF)
This implies:
ar (ABFC) = ar ($\triangle$ADF)
Hence, Proved.
Alternate Solution:
Consider triangles $\triangle ABC$ and $\triangle ABF$.
They lie on the same base AB.
Since ABCD is a parallelogram, $AB \parallel DC$. As DC is produced to F, the line CF is parallel to AB. Thus, $\triangle ABC$ and $\triangle ABF$ are between the same parallels AB and CF.
Therefore, their areas are equal.
ar($\triangle ABC$) = ar($\triangle ABF$)
... (iv)
Now consider the triangles $\triangle ADC$ and $\triangle FBC$.
In $\triangle ABE$ and $\triangle FCE$,
$\angle AEB = \angle FEC$
(Vertically opposite angles)
$\angle EAB = \angle EFC$
(Alternate interior angles as $AB \parallel DF$)
So, $\triangle ABE \sim \triangle FCE$.
Let's go back to our main equation.
We need to prove ar(ADF) = ar(ABFC).
ar(ADF) = ar(ABCD) + ar($\triangle BCF$)
ar(ABFC) = ar($\triangle ABF$) + ar($\triangle BCF$)
So, we need to prove that ar(ABCD) = ar($\triangle ABF$).
We know ar(ABCD) = 2 $\times$ ar($\triangle ABC$).
From (iv), ar($\triangle ABF$) = ar($\triangle ABC$).
This means we would need to prove ar(ABCD) = ar($\triangle ABC$), which is incorrect.
Let's re-examine the decomposition of area:
ar(ADF) = ar(trapezium ABCF) + ar($\triangle CDF$). No, this is incorrect.
ar(ADF) = ar(trapezium ABFD) - ar($\triangle ABF$).
The first proof remains the simplest and most direct method.
Question 2. The diagonals of a parallelogram ABCD intersect at a point O. Through O, a line is drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area.
Answer:
Given:
A parallelogram ABCD whose diagonals AC and BD intersect at a point O.
A line passes through O and intersects the side AD at P and the side BC at Q.
To Prove:
The line segment PQ divides the parallelogram ABCD into two parts of equal area. That is, ar (ABQP) = ar (PQCD).
Construction:
The figure as given is sufficient for the proof.
Proof:
We know that the diagonals of a parallelogram bisect each other. Therefore, for parallelogram ABCD, O is the mid-point of both diagonals AC and BD.
OA = OC
(Diagonals bisect each other)
Now, let's consider the triangles $\triangle AOP$ and $\triangle COQ$.
$\angle PAO = \angle QCO$
(Alternate interior angles, since $AD \parallel BC$ and AC is the transversal)
OA = OC
(Proved above)
$\angle AOP = \angle COQ$
(Vertically opposite angles)
By the Angle-Side-Angle (ASA) congruence criterion, we have:
$\triangle AOP \cong \triangle COQ$
Since congruent figures have equal areas, we can conclude that:
ar($\triangle AOP$) = ar($\triangle COQ$)
... (i)
We also know that a diagonal of a parallelogram divides it into two triangles of equal area. For the diagonal AC:
ar($\triangle ABC$) = ar($\triangle ADC$) = $\frac{1}{2}$ ar(ABCD)
... (ii)
The area of trapezium ABQP is the sum of the areas of $\triangle ABQ$ and $\triangle APQ$. The area of trapezium PQCD is the sum of the areas of $\triangle PQC$ and $\triangle PCD$.
Let's use the decomposition based on diagonal AC.
ar(ABQP) = ar(ABQ) + ar(APQ)
Area of trapezium ABQP = ar(quadrilateral ABCO) + ar($\triangle AOP$) - ar($\triangle COQ$).
Let's try: ar(ABQP) = ar(ΔABC) + ar(ΔACP) - ar(ΔBCP)
Let's revisit the sum of areas from the figure.
ar(PQCD) = ar($\triangle ADC$) - ar($\triangle AOP$) + ar($\triangle COQ$)
ar(ABQP) = ar($\triangle ABC$) + ar($\triangle AOP$) - ar($\triangle COQ$)
Using equation (i), we know ar($\triangle AOP$) = ar($\triangle COQ$).
So, ar(PQCD) = ar($\triangle ADC$) - ar($\triangle AOP$) + ar($\triangle AOP$) = ar($\triangle ADC$).
And, ar(ABQP) = ar($\triangle ABC$) + ar($\triangle COQ$) - ar($\triangle COQ$) = ar($\triangle ABC$).
Using equation (ii), we know ar($\triangle ABC$) = ar($\triangle ADC$).
Therefore, ar(ABQP) = ar(PQCD).
Thus, the line PQ divides the parallelogram into two parts of equal area.
Hence, Proved.
Question 3. The medians BE and CF of a triangle ABC intersect at G. Prove that the area of ∆ GBC = area of the quadrilateral AFGE.
Answer:
Given:
A triangle $\triangle ABC$.
BE and CF are the medians of $\triangle ABC$. This means E is the mid-point of AC, and F is the mid-point of AB.
The medians BE and CF intersect at point G.
To Prove:
Area of $\triangle$GBC = Area of the quadrilateral AFGE.
ar ($\triangle$GBC) = ar (AFGE).
Proof:
We know that a median of a triangle divides it into two triangles of equal area.
Since BE is the median of $\triangle ABC$ to the side AC:
ar ($\triangle$ABE) = ar ($\triangle$CBE)
... (i)
Similarly, since CF is the median of $\triangle ABC$ to the side AB:
ar ($\triangle$ACF) = ar ($\triangle$BCF)
... (ii)
From equation (i), we can also say that:
ar ($\triangle$ABE) = $\frac{1}{2}$ ar ($\triangle$ABC)
... (iii)
From equation (ii), we can also say that:
ar ($\triangle$BCF) = $\frac{1}{2}$ ar ($\triangle$ABC)
... (iv)
From equations (iii) and (iv), we can conclude that the areas of $\triangle ABE$ and $\triangle BCF$ are equal:
ar ($\triangle$ABE) = ar ($\triangle$BCF)
... (v)
From the figure, we can decompose the areas of these triangles:
ar ($\triangle$ABE) = ar (quadrilateral AFGE) + ar ($\triangle$GBF)
ar ($\triangle$BCF) = ar ($\triangle$GBC) + ar ($\triangle$GBF)
Substituting these expressions back into equation (v):
ar (AFGE) + ar ($\triangle$GBF) = ar ($\triangle$GBC) + ar ($\triangle$GBF)
Now, subtracting the area of the common triangle, ar ($\triangle$GBF), from both sides of the equation, we get:
ar (AFGE) = ar ($\triangle$GBC)
Hence, Proved.
Question 4. In Fig. 9.24, CD || AE and CY || BA. Prove that ar (CBX) = ar (AXY)
Answer:
Given:
In the given figure, we have two conditions:
1. $CD \parallel AE$
2. $CY \parallel BA$
To Prove:
ar ($\triangle$CBX) = ar ($\triangle$AXY).
Proof:
We know that triangles on the same base and between the same parallels are equal in area.
Let's consider the triangles $\triangle ABC$ and $\triangle ABY$.
These two triangles lie on the same base AB.
They also lie between the same parallel lines AB and CY, because it is given that $CY \parallel BA$.
Therefore, according to the theorem, their areas must be equal.
ar ($\triangle$ABC) = ar ($\triangle$ABY)
... (i)
From the figure, we can see that the area of $\triangle ABC$ is the sum of the areas of $\triangle ABX$ and $\triangle CBX$.
ar ($\triangle$ABC) = ar ($\triangle$ABX) + ar ($\triangle$CBX)
Similarly, the area of $\triangle ABY$ is the sum of the areas of $\triangle ABX$ and $\triangle AXY$.
ar ($\triangle$ABY) = ar ($\triangle$ABX) + ar ($\triangle$AXY)
Now, substitute these expressions back into equation (i):
ar ($\triangle$ABX) + ar ($\triangle$CBX) = ar ($\triangle$ABX) + ar ($\triangle$AXY)
Subtracting the common area, ar ($\triangle$ABX), from both sides of the equation, we get:
ar ($\triangle$CBX) = ar ($\triangle$AXY)
Hence, Proved.
Note: The condition $CD \parallel AE$ is additional information and is not required for this proof.
Question 5. ABCD is a trapezium in which AB || DC, DC = 30 cm and AB = 50 cm. If X and Y are, respectively the mid-points of AD and BC, prove that ar (DCYX) = $\frac{7}{9}$ ar (XYBA).
Answer:
Given:
A trapezium ABCD with $AB \parallel DC$.
Length of the parallel side, $DC = 30$ cm.
Length of the parallel side, $AB = 50$ cm.
X is the mid-point of the side AD.
Y is the mid-point of the side BC.
To Prove:
ar (DCYX) = $\frac{7}{9}$ ar (XYBA).
Construction:
Join the points D and Y. Extend the line segment DY to meet the produced line AB at a point P.
Proof:
First, we will prove the congruence of $\triangle DCY$ and $\triangle PBY$.
In $\triangle DCY$ and $\triangle PBY$:
$\angle DCY = \angle PBY$
(Alternate interior angles, since $DQ \parallel AP$ and BC is the transversal)
$CY = BY$
(Given, Y is the mid-point of BC)
$\angle DYC = \angle PYB$
(Vertically opposite angles)
By the Angle-Side-Angle (ASA) congruence rule:
$\triangle DCY \cong \triangle PBY$
By CPCTC (Corresponding Parts of Congruent Triangles are Congruent), we have:
$DC = PB$ and $DY = YP$
... (i)
Since $DC = 30$ cm, we get $PB = 30$ cm.
Now, consider the large triangle $\triangle ADP$.
We are given that X is the mid-point of AD.
From our congruence result (i), we have $DY=YP$, which means Y is the mid-point of the side DP.
By the Mid-point Theorem, the line segment joining the mid-points of two sides of a triangle is parallel to the third side and is half of its length.
Therefore, in $\triangle ADP$ with mid-points X and Y:
$XY \parallel AP$ and $XY = \frac{1}{2} AP$
Let's calculate the length of AP:
$AP = AB + BP = 50 \text{ cm} + 30 \text{ cm} = 80 \text{ cm}$.
So, the length of XY is:
$XY = \frac{1}{2} \times 80 = 40$ cm.
The line segment XY divides the trapezium ABCD into two smaller trapeziums: DCYX and XYBA.
Since XY joins the mid-points of the non-parallel sides, it bisects the height of the trapezium ABCD. Let the height of the smaller trapeziums be $h$.
Now we find the area of the trapezium DCYX.
The parallel sides are DC and XY.
ar (DCYX) = $\frac{1}{2} \times (\text{sum of parallel sides}) \times \text{height}$
ar (DCYX) = $\frac{1}{2} \times (DC + XY) \times h = \frac{1}{2} \times (30 + 40) \times h \ $$ = \frac{1}{2} \times 70 \times h \ $$ = 35h$ cm².
Now we find the area of the trapezium XYBA.
The parallel sides are XY and BA.
ar (XYBA) = $\frac{1}{2} \times (XY + BA) \times h = \frac{1}{2} \times (40 + 50) \times h \ $$ = \frac{1}{2} \times 90 \times h \ $$ = 45h$ cm².
Finally, we find the ratio of the areas:
$\frac{\text{ar (DCYX)}}{\text{ar (XYBA)}} = \frac{35h}{45h} = \frac{35}{45} = \frac{7 \times 5}{9 \times 5} = \frac{7}{9}$
Therefore, ar (DCYX) = $\frac{7}{9}$ ar (XYBA).
Hence, Proved.
Question 6. In ∆ ABC, if L and M are the points on AB and AC, respectively such that LM || BC. Prove that ar (LOB) = ar (MOC)
Answer:
Given:
A triangle $\triangle ABC$.
L and M are points on the sides AB and AC, respectively.
The line segment LM is parallel to the side BC, i.e., $LM \parallel BC$.
The line segments LC and MB intersect at a point O.
To Prove:
The area of $\triangle$LOB is equal to the area of $\triangle$MOC.
ar ($\triangle$LOB) = ar ($\triangle$MOC).
Proof:
We will use the theorem which states that triangles on the same base and between the same parallels are equal in area.
Consider the triangles $\triangle LBC$ and $\triangle MBC$.
These two triangles lie on the same base BC.
They also lie between the same parallel lines BC and LM, as it is given that $LM \parallel BC$.
Therefore, according to the theorem, the areas of these two triangles are equal.
ar ($\triangle$LBC) = ar ($\triangle$MBC)
... (i)
From the figure, we can see that the triangle $\triangle BOC$ is a common part of both $\triangle LBC$ and $\triangle MBC$.
We can decompose the areas of the larger triangles as follows:
ar ($\triangle$LBC) = ar ($\triangle$LOB) + ar ($\triangle$BOC)
ar ($\triangle$MBC) = ar ($\triangle$MOC) + ar ($\triangle$BOC)
Substituting these expressions into equation (i), we get:
ar ($\triangle$LOB) + ar ($\triangle$BOC) = ar ($\triangle$MOC) + ar ($\triangle$BOC)
Now, subtracting the area of the common triangle, ar ($\triangle$BOC), from both sides of the equation:
ar ($\triangle$LOB) = ar ($\triangle$MOC)
Hence, Proved.
Question 7. In Fig. 9.25, ABCDE is any pentagon. BP drawn parallel to AC meets DC produced at P and EQ drawn parallel to AD meets CD produced at Q. Prove that ar (ABCDE) = ar (APQ).
Answer:
Given:
ABCDE is a pentagon.
A line through B parallel to AC (i.e., $BP \parallel AC$) meets the line DC produced at P.
A line through E parallel to AD (i.e., $EQ \parallel AD$) meets the line CD produced at Q.
To Prove:
The area of the pentagon ABCDE is equal to the area of the triangle APQ.
ar (ABCDE) = ar ($\triangle$APQ).
Proof:
The proof is based on the principle that triangles on the same base and between the same parallels are equal in area.
First, let's consider the triangles $\triangle ABC$ and $\triangle APC$.
They lie on the same base AC.
They are also between the same parallel lines AC and BP, as it is given that $BP \parallel AC$.
Therefore, their areas are equal.
ar ($\triangle$ABC) = ar ($\triangle$APC)
... (i)
Next, let's consider the triangles $\triangle ADE$ and $\triangle ADQ$.
They lie on the same base AD.
They are also between the same parallel lines AD and EQ, as it is given that $EQ \parallel AD$.
Therefore, their areas are equal.
ar ($\triangle$ADE) = ar ($\triangle$ADQ)
... (ii)
Now, let's analyze the area of the pentagon ABCDE. It is the sum of the areas of three triangles:
ar (ABCDE) = ar ($\triangle$ABC) + ar ($\triangle$ACD) + ar ($\triangle$ADE)
Using the results from our equations (i) and (ii), we can substitute ar ($\triangle$APC) for ar ($\triangle$ABC) and ar ($\triangle$ADQ) for ar ($\triangle$ADE):
ar (ABCDE) = ar ($\triangle$APC) + ar ($\triangle$ACD) + ar ($\triangle$ADQ)
From the figure, we can see that the sum of the areas of $\triangle$APC, $\triangle$ACD, and $\triangle$ADQ is equal to the area of the large triangle $\triangle$APQ.
ar ($\triangle$APC) + ar ($\triangle$ACD) + ar ($\triangle$ADQ) = ar ($\triangle$APQ)
Therefore, we can conclude that:
ar (ABCDE) = ar ($\triangle$APQ)
Hence, Proved.
Question 8. If the medians of a ∆ ABC intersect at G, show that ar (AGB) = ar (AGC) = ar (BGC) = $\frac{1}{3}$ ar (ABC)
Answer:
Given:
A triangle $\triangle$ABC.
The medians AD, BE, and CF of $\triangle$ABC intersect at a point G (the centroid).
To Prove:
ar ($\triangle$AGB) = ar ($\triangle$AGC) = ar ($\triangle$BGC) = $\frac{1}{3}$ ar ($\triangle$ABC).
Proof:
We know that a median of a triangle divides it into two triangles of equal area.
In $\triangle$ABC, AD is the median to the side BC.
ar ($\triangle$ABD) = ar ($\triangle$ACD)
... (i)
Now, consider $\triangle$GBC. Since G lies on the median AD, the line segment GD connects vertex G to the mid-point D of the opposite side BC. Therefore, GD is the median of $\triangle$GBC.
ar ($\triangle$GBD) = ar ($\triangle$GCD)
... (ii)
Subtracting equation (ii) from equation (i), we get:
ar ($\triangle$ABD) - ar ($\triangle$GBD) = ar ($\triangle$ACD) - ar ($\triangle$GCD)
From the figure, we can see that:
ar ($\triangle$ABD) - ar ($\triangle$GBD) = ar ($\triangle$AGB)
ar ($\triangle$ACD) - ar ($\triangle$GCD) = ar ($\triangle$AGC)
Therefore, we can conclude that:
ar ($\triangle$AGB) = ar ($\triangle$AGC)
... (iii)
Similarly, we can consider the median BE of $\triangle$ABC and show that:
ar ($\triangle$AGB) = ar ($\triangle$BGC)
... (iv)
From equations (iii) and (iv), we have proved that the areas of the three triangles are equal:
ar ($\triangle$AGB) = ar ($\triangle$AGC) = ar ($\triangle$BGC)
... (v)
The area of the entire triangle $\triangle$ABC is the sum of the areas of these three triangles:
ar ($\triangle$ABC) = ar ($\triangle$AGB) + ar ($\triangle$AGC) + ar ($\triangle$BGC)
Using the result from equation (v), we can replace the areas of $\triangle$AGC and $\triangle$BGC with the area of $\triangle$AGB:
ar ($\triangle$ABC) = ar ($\triangle$AGB) + ar ($\triangle$AGB) + ar ($\triangle$AGB)
ar ($\triangle$ABC) = 3 $\times$ ar ($\triangle$AGB)
Rearranging this equation gives:
ar ($\triangle$AGB) = $\frac{1}{3}$ ar ($\triangle$ABC)
Combining this with our earlier result from equation (v), we get the final proof:
ar ($\triangle$AGB) = ar ($\triangle$AGC) = ar ($\triangle$BGC) = $\frac{1}{3}$ ar ($\triangle$ABC)
Hence, Proved.
Question 9. In Fig. 9.26, X and Y are the mid-points of AC and AB respectively, QP || BC and CYQ and BXP are straight lines. Prove that ar (ABP) = ar (ACQ).
Answer:
Given:
In $\triangle ABC$, Y is the mid-point of side AB and X is the mid-point of side AC.
A line segment QP is drawn such that $QP \parallel BC$, with points P and Q on the lines BXP and CYQ respectively.
BXP and CYQ are straight lines.
To Prove:
ar ($\triangle$ABP) = ar ($\triangle$ACQ).
Proof:
In $\triangle ABC$, since Y and X are the mid-points of sides AB and AC respectively, by the Mid-point Theorem, the line segment XY is parallel to the third side BC.
$XY \parallel BC$
... (i)
We are given that $QP \parallel BC$. From this and equation (i), we can conclude that all three lines are parallel to each other:
$QP \parallel XY \parallel BC$
Now, consider the triangles $\triangle XYB$ and $\triangle XYC$.
They lie on the same base XY and are between the same parallel lines XY and BC.
We know that triangles on the same base and between the same parallels are equal in area.
ar($\triangle XYB$) = ar($\triangle XYC$)
... (ii)
Next, consider the triangles $\triangle PXY$ and $\triangle QXY$.
They lie on the same base XY and are between the same parallel lines XY and QP.
Therefore, their areas are also equal.
ar($\triangle PXY$) = ar($\triangle QXY$)
... (iii)
Adding equation (ii) and equation (iii), we get:
ar($\triangle XYB$) + ar($\triangle PXY$) = ar($\triangle XYC$) + ar($\triangle QXY$)
From the figure, the sum of the areas on the left-hand side is the area of the quadrilateral PXYB.
ar($\triangle XYB$) + ar($\triangle PXY$) = ar(quadrilateral PXYB)
Similarly, the sum of the areas on the right-hand side is the area of the quadrilateral QXYC.
ar($\triangle XYC$) + ar($\triangle QXY$) = ar(quadrilateral QXYC)
Thus, we have shown that:
ar(PXYB) = ar(QXYC)
... (iv)
Now, let's add the area of the common triangle, $\triangle AXY$, to both sides of equation (iv):
ar($\triangle AXY$) + ar(PXYB) = ar($\triangle AXY$) + ar(QXYC)
Observing the figure again:
ar($\triangle AXY$) + ar(PXYB) = ar($\triangle ABP$)
ar($\triangle AXY$) + ar(QXYC) = ar($\triangle ACQ$)
Therefore, we can conclude that:
ar ($\triangle$ABP) = ar ($\triangle$ACQ)
Hence, Proved.
Question 10. In Fig. 9.27, ABCD and AEFD are two parallelograms. Prove that ar (PEA) = ar (QFD).
[Hint: Join PD].
Answer:
Given:
ABCD and AEFD are two parallelograms sharing the common side AD.
To Prove:
ar ($\triangle$PEA) = ar ($\triangle$QFD).
Proof:
We are given that ABCD and AEFD are parallelograms. We will use the properties of parallelograms to establish the result.
First, we will prove that the quadrilateral APQD is also a parallelogram.
In parallelogram ABCD, opposite sides are parallel. Therefore,
$AB \parallel DC$
(Opposite sides of parallelogram ABCD)
Since AP is a part of the line segment AB and DQ is a part of the line segment DC, it follows that:
$AP \parallel DQ$
... (i)
In parallelogram AEFD, opposite sides are parallel. Therefore,
$EF \parallel AD$
(Opposite sides of parallelogram AEFD)
Since PQ is a part of the line segment containing EF, it follows that:
$PQ \parallel AD$
... (ii)
From equations (i) and (ii), since both pairs of opposite sides of the quadrilateral APQD are parallel, APQD is a parallelogram.
Now, let's compare the areas of parallelogram AEFD and parallelogram APQD.
Both of these parallelograms lie on the same base AD.
They also lie between the same parallel lines AD and EQ (since $AD \parallel EF$ and the points E, P, F, Q are collinear).
We know that parallelograms on the same base and between the same parallels are equal in area.
Therefore,
ar(AEFD) = ar(APQD)
... (iii)
From the figure, we can decompose the areas of these two parallelograms. The quadrilateral APFD is a common part of both.
ar(AEFD) = ar($\triangle$PEA) + ar(quadrilateral APFD)
ar(APQD) = ar($\triangle$QFD) + ar(quadrilateral APFD)
Substituting these expressions into equation (iii), we get:
ar($\triangle$PEA) + ar(APFD) = ar($\triangle$QFD) + ar(APFD)
Subtracting the area of the common quadrilateral, ar(APFD), from both sides of the equation, we get:
ar($\triangle$PEA) = ar($\triangle$QFD)
Hence, Proved.

